Martin Gardner - Mathematische Planetenzauberei. Space Puzzles.

Die Planetoiden umkreisen die Sonne in Zeiträumen, die von zwei bis zwölf Jahre reichen. Viele ihrer Bahnen sind stark geneigt gegen die ›Ekliptik‹ – die Ebene, in der die Erde umläuft. Zum Beispiel ist Hidalgos Umlaufbahn um fast 45 Grad gegen die Ekliptik geneigt.

Nur ein Planetoid, Vesta – ihr Durchmesser ist rund 400 km – kann mit dem bloßen Auge gesehen werden. Das ist nicht so, weil Vesta so groß ist oder der Erde so näherkommt, sondern weil ihre Oberfläche mehr Licht reflektiert als andere große Planetoiden. Die Astronomen wissen nicht warum, aber wahrscheinlich ist das so, weil Vesta eine ungewöhnlich glatte Oberfläche hat. Kein Planetoid ist groß genug, um eine Atmosphäre halten zu können. Auf Ceres, dem größten, würde ein Junge von hundert Pfund weniger als vier Pfund wiegen. Auf kleineren Planetoiden könnte ein Astronaut leicht mit genügend großer Geschwindigkeit hochspringen, um in den Raum zu entkommen und nie zurückzukehren. Von besonderem Interesse für die Astronomen sind zwei Gruppen von Planetoiden, die als die Trojaner bekannt sind. Sie haben diesen Namen erhalten, weil jeder aus dieser Gruppe, der identifiziert worden ist, benannt ist nach einem Krieger aus Homers I 1 i a s, einem epischen Gedicht, das von dem berühmten Trojanischen Krieg zwischen Griechenland und Troja erzählt. Um zu erklären, warum die Trojaner von solcher Wichtigkeit sind, müssen wir bis zu dem Jahr 1772 zurückgehen, als der französische Mathematiker und Astronom Graf Joseph Louis Lagrange eine erregende Entdeckung machte. Er bewies mathematisch, daß zwei Körper (oder Gruppen von Körpern) die Sonne so umkreisen könnten, daß sie sich ständig an zwei Ecken eines gleichseitigen Dreiecks befänden, mit der Sonne an der dritten Ecke des Dreiecks. Mit anderen Worten, die dreieckige Anordnung würde stabil bleiben. Das war nichts als eine mathematisch-astronomische Kuriosität, bis 1906 Astronomen einen Planetoiden, Achilles genannt, an einem ›La-grange-Punkt‹ fanden. Die anderen zwei Ecken des gleichseitigen Dreiecks werden von der Sonne und Jupiter eingenommen.

Seit 1906 wurden mehr als ein Dutzend Planetoide an Jupiters beiden Lagrange-Punkten gefunden. Die eine Gruppe eilt Jupiter voraus, die andere folgt nach. Wie in der Abbildung gezeichnet, bleiben diese beiden Planetoidengruppen ständig an den Ecken zweier riesiger gleichseitiger Dreiecke gefesselt, während Jupiter um die Sonne kreist. Sie liefern einen dramatischen Beweis für die Richtigkeit von Lagranges Berechnungen.

Frage 29:

Ist es möglich, daß eines Tages die Erde mit einem großen Planetoiden zusammenstoßen könnte?

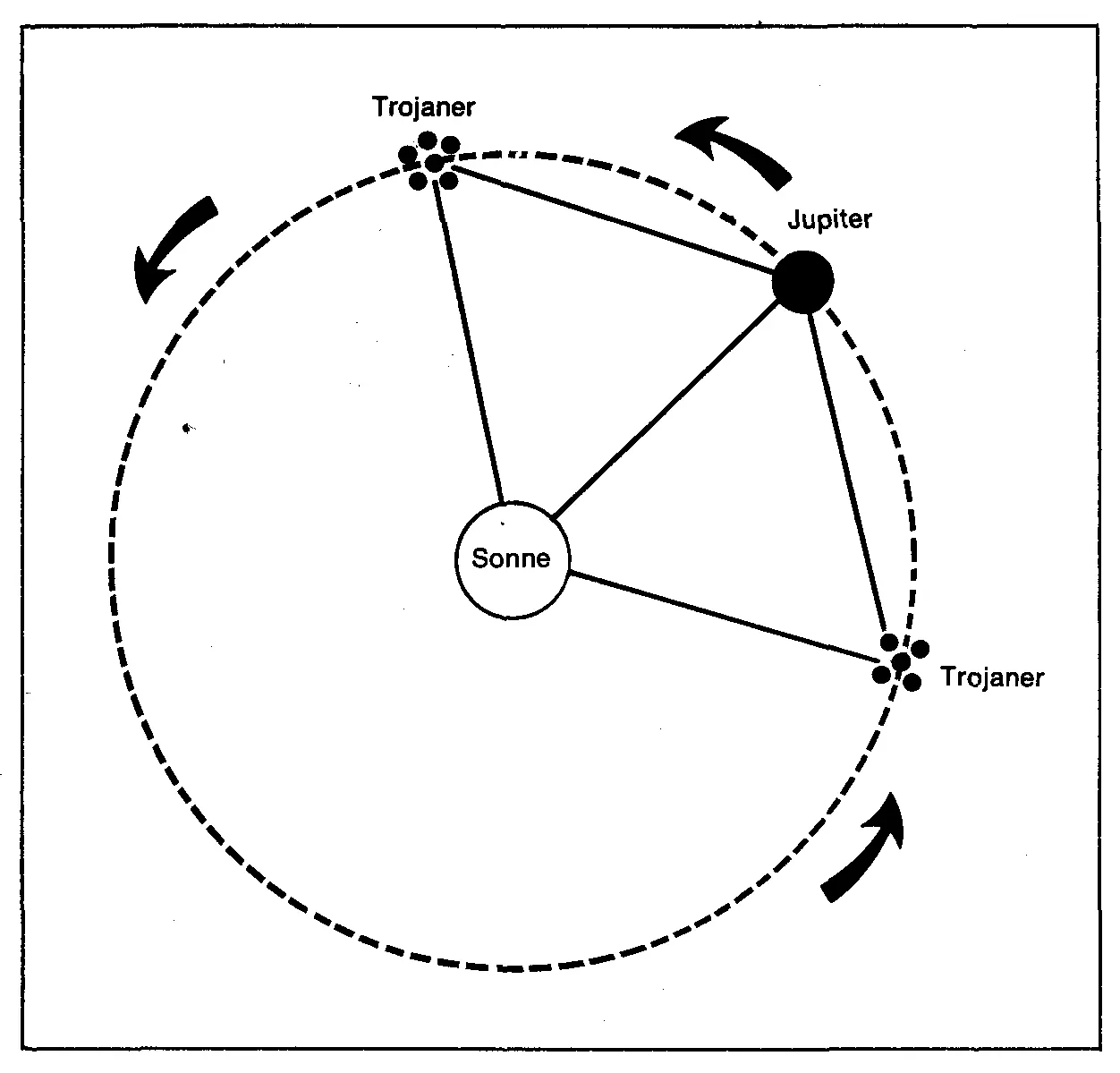
Die Lagrange-Punkte des Jupiter und die zwei Gruppen von Trojanern.

Frage 30:

Der Planetoid, der als 694ster entdeckt wurde, wurde von seinem Entdecker Ekard genannt. (Wer immer einen neuen Planetoiden findet, kann ihm jeden Namen geben, den er möchte. Einer heißt Chicago, und ein anderer, Marlene, wurde nach der berühmten Filmschauspielerin Marlene Dietrich benannt.) Ekard ist ein seltsamer Name. Können Sie erraten, was er bedeutet?

Einige Jahre bevor die Gebrüder Wright ihren ersten erfolgreichen Flug mit einem Flugzeug machten, gab es viele intelligente Leute, Naturwissenschaftler eingeschlossen, die schlankweg behaupteten, funktionstüchtige Flugmaschinen könnten nie gebaut werden. Simon Newcomb, ein amerikanischer Astronom, äußerte sich besonders verächtlich: »Sehr wahrscheinlich«, sagte er, »wird die wirksamste Flugmaschine von einer ungeheuren Zahl kleiner Vögel getragen werden.«

Dieser Mangel an Phantasie veranlaßte viele Naturwissenschaftler, ähnlich befremdliche Vorhersagen über die Unmöglichkeit der Raumfahrt zu machen. Der berühmte Astronom der Universität von Chicago, Forest Ray Moulton, schrieb in einem einst vielbenutzten Collegelehrbuch Astronomie (1931) auf Seite 296:

Manch eine Geschichte ist geschrieben worden über einige wunderbare Reisen zum Mond oder Mars… Es gibt jedoch keine Hoffnung, daß ein derartiger Wunsch je in die Wirklichkeit umgesetzt wird. Die Schwierigkeit, der Erdanziehung zu entkommen, ist unüberwindlich; das Problem, das Gefährt durch den Himmelsraum zu lenken, und das des sanften Abstieges bis zur Ruhe auf der Oberfläche eines weiteren Körpers mit Schwerkraft sind gleicherweise schrecklich. Nur jene, die nicht mit den dabei beteiligten physikalischen Kräften vertraut sind, können glauben, daß solche Abenteuer jemals aus dem Reich der Phantasie heraustreten werden.

Die großen frühen Science-Fiction-Autoren jedoch zweifelten nicht einen Augenblick daran, daß Raumschiffe der Erde eines Tages den Mond und die Planeten erforschen würden. Jules Vernes bekannter Roman Reise um den Mond (1870), eine Fortsetzung seines früheren Romans über den Bau eines Raumschiffes, erzählt von einem Flug von drei Personen um den Mond in einer Kapsel, die von Tampa in Florida aus abgeschossen wird. Nicht weit davon entfernt befindet sich jetzt das Weltraumzentrum Cape Canaveral (früher Cape Kennedy). Die Landefähre von Apollo 11, die die Astronauten zum ersten Mal zur Mondoberfläche brachte, hieß Columbia nach Vernes phantastischem Raumschiff Columbiade. Die Columbiade stürzte sogar in den Pazifik, wo die Astronauten von einem US-Dampfer geborgen wurden.

Diese zwei Illustrationen aus der Originalausgabe von Jules Vernes »Reise um den Mond« zeigen das Raumschiff, die Columbiade, kurz vor der Landung auf dem Mond (links) und das Schiff und seine drei Passagiere, nachdem sie gelandet sind. Es ist interessant, die Vorstellung eines Künstlers aus dem neunzehnten Jahrhundert von einer Mondlandung mit einer Photographie einer tatsächlichen Landung der Mondlandefähre ›Intrepid‹ während der Reise von Apollo 12 (siehe Seite 72) zu vergleichen.

Es gibt keinen Grund, die bekannte dramatische Geschichte des modernen Raumfluges hier durchzugehen. Stattdessen will ich einige Ausschnitte aus Die befreite Welt wiedergeben, einem Roman von H. G. Wells, einem weiteren berühmten Pionier der Science Fiction. Der Roman wurde 1914 veröffentlicht. Es ist das prophetischste von Wells’ erzählerischen Werken, weil es von der Kernspaltung berichtet und wie diese Kenntnis genutzt wurde, um zu bauen, was Wells die ›Atombombe‹ nannte – Bomben, die in einem verheerenden Krieg geworfen wurden, von dem Wells sich vorstellte, daß er nahe der Mitte des zwanzigsten Jahrhunderts aufkäme. Hier folgen einige Zeilen aus dem letzten Kapitel des Romans. Sie sind eine erstaunliche Vorwegnahme des Weltraum-Zeitalters, eines Zeitalters, das viel früher begann, als Wells erwartet hatte.

Die zweite Mondlandung, die von Apollo 12, steht kurz bevor. Die Mondlandefähre ›Intrepid‹ mit den Astronauten Charles Conrad Jr. und Alan Bean an Bord steigt zu dem Landeplatz ab. Die Mondlandefähre hat sich vom Kommandoteil, dem ›Yankee Clipper‹, getrennt, der Richard Gordon beherbergt.

»Dieser runde Planet ist nicht länger an uns gekettet wie die Kugel eines Galeerensklaven… In einer nahen Zukunft werden Menschen, die wissen, wie man die unbekannte Schwerkraft, die geänderten Drucke, die verdünnten ungewohnten Gase und die ganze furchterregende Fremdheit des Raumes erträgt, sich von dieser Erde wegwagen. Dieser Globus wird uns nicht länger genügen; unser Geist wird nach den Sternen greifen…«