Ray Kurzweil - How to Create a Mind - The Secret of Human Thought Revealed

Oxford University computational neuroscientist Anders Sandberg (born in 1972) and Swedish philosopher Nick Bostrom (born in 1973) have written the comprehensive Whole Brain Emulation: A Roadmap , which details the requirements for simulating the human brain (and other types of brains) at different levels of specificity from high-level functional models to simulating molecules. 8 The report does not provide a timeline, but it does describe the requirements to simulate different types of brains at varying levels of precision in terms of brain scanning, modeling, storage, and computation. The report projects ongoing exponential gains in all of these areas of capability and argues that the requirements to simulate the human brain at a high level of detail are coming into place.

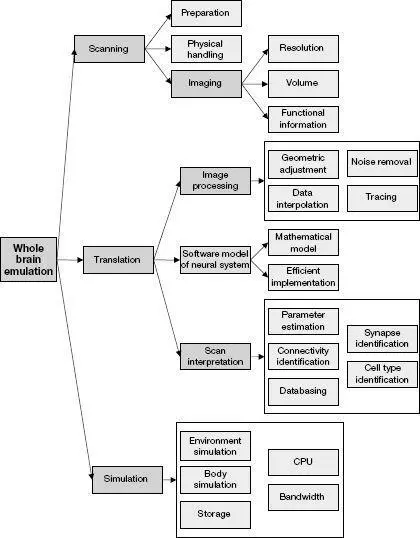
An outline of the technological capabilities needed for whole brain emulation, in Whole Brain Emulation: A Roadmap by Anders Sandberg and Nick Bostrom.

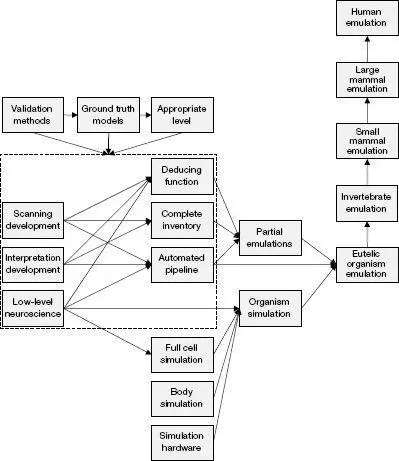
An outline of Whole Brain Emulation: A Roadmap by Anders Sandberg and Nick Bostrom.

In 1964, at the age of sixteen, I wrote to Frank Rosenblatt (1928–1971), a professor at Cornell University, inquiring about a machine called the Mark 1 Perceptron. He had created it four years earlier, and it was described as having brainlike properties. He invited me to visit him and try the machine out.

The Perceptron was built from what he claimed were electronic models of neurons. Input consisted of values arranged in two dimensions. For speech, one dimension represented frequency and the other time, so each value represented the intensity of a frequency at a given point in time. For images, each point was a pixel in a two-dimensional image. Each point of a given input was randomly connected to the inputs of the first layer of simulated neurons. Every connection had an associated synaptic strength, which represented its importance, and which was initially set at a random value. Each neuron added up the signals coming into it. If the combined signal exceeded a particular threshold, the neuron fired and sent a signal to its output connection; if the combined input signal did not exceed the threshold, the neuron did not fire, and its output was zero. The output of each neuron was randomly connected to the inputs of the neurons in the next layer. The Mark 1 Perceptron had three layers, which could be organized in a variety of configurations. For example, one layer might feed back to an earlier one. At the top layer, the output of one or more neurons, also randomly selected, provided the answer. (For an algorithmic description of neural nets, see this endnote.) 9

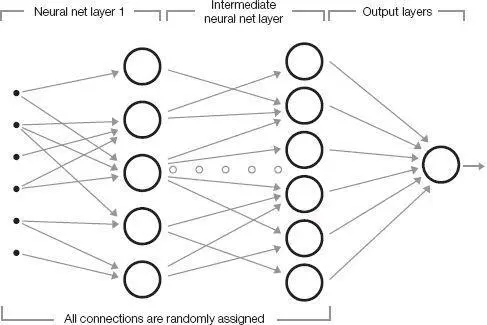
Since the neural net wiring and synaptic weights are initially set randomly, the answers of an untrained neural net are also random. The key to a neural net, therefore, is that it must learn its subject matter, just like the mammalian brains on which it’s supposedly modeled. A neural net starts out ignorant; its teacher—which may be a human, a computer program, or perhaps another, more mature neural net that has already learned its lessons—rewards the student neural net when it generates the correct output and punishes it when it does not. This feedback is in turn used by the student neural net to adjust the strength of each interneuronal connection. Connections that are consistent with the correct answer are made stronger. Those that advocate a wrong answer are weakened.

Over time the neural net organizes itself to provide the correct answers without coaching. Experiments have shown that neural nets can learn their subject matter even with unreliable teachers. If the teacher is correct only 60 percent of the time, the student neural net will still learn its lessons with an accuracy approaching 100 percent.

However, limitations in the range of material that the Perceptron was capable of learning quickly became apparent. When I visited Professor Rosenblatt in 1964, I tried simple modifications to the input. The system was set up to recognize printed letters, and would recognize them quite accurately. It did a fairly good job of autoassociation (that is, it could recognize the letters even if I covered parts of them), but fared less well with invariance (that is, generalizing over size and font changes, which confused it).

During the last half of the 1960s, these neural nets became enormously popular, and the field of “connectionism” took over at least half of the artificial intelligence field. The more traditional approach to AI, meanwhile, included direct attempts to program solutions to specific problems, such as how to recognize the invariant properties of printed letters.

Another person I visited in 1964 was Marvin Minsky (born in 1927), one of the founders of the artificial intelligence field. Despite having done some pioneering work on neural nets himself in the 1950s, he was concerned with the great surge of interest in this technique. Part of the allure of neural nets was that they supposedly did not require programming—they would learn solutions to problems on their own. In 1965 I entered MIT as a student with Professor Minsky as my mentor, and I shared his skepticism about the craze for “connectionism.”

In 1969 Minsky and Seymour Papert (born in 1928), the two cofounders of the MIT Artificial Intelligence Laboratory, wrote a book called Perceptrons , which presented a single core theorem: specifically, that a Perceptron was inherently incapable of determining whether or not an image was connected. The book created a firestorm. Determining whether or not an image is connected is a task that humans can do very easily, and it is also a straightforward process to program a computer to make this discrimination. The fact that Perceptrons could not do so was considered by many to be a fatal flaw.

Two images from the cover of the book Perceptrons by Marvin Minsky and Seymour Papert. The top image is not connected (that is, the dark area consists of two disconnected parts). The bottom image is connected. A human can readily determine this, as can a simple software program. A feedforward Perceptron such as Frank Rosenblatt’s Mark 1 Perceptron cannot make this determination.

Perceptrons , however, was widely interpreted to imply more than it actually did. Minsky and Papert’s theorem applied only to a particular type of neural net called a feedforward neural net (a category that does include Rosenblatt’s Perceptron); other types of neural nets did not have this limitation. Still, the book did manage to largely kill most funding for neural net research during the 1970s. The field did return in the 1980s with attempts to use what were claimed to be more realistic models of biological neurons and ones that avoided the limitations implied by the Minsky-Papert Perceptron theorem. Nevertheless, the ability of the neocortex to solve the invariance problem, a key to its strength, was a skill that remained elusive for the resurgent connectionist field.

In the early 1980s I started a project devoted to another classical pattern recognition problem: understanding human speech. At first, we used traditional AI approaches by directly programming expert knowledge about the fundamental units of speech—phonemes—and rules from linguists on how people string phonemes together to form words and phrases. Each phoneme has distinctive frequency patterns. For example, we knew that vowels such as “e” and “ah” are characterized by certain resonant frequencies called formants, with a characteristic ratio of formants for each phoneme. Sibilant sounds such as “z” and “s” are characterized by a burst of noise that spans many frequencies.