Нассим Талеб - The Black Swan. The Impact of the Highly Improbable

Poincaré wrote that one of his friends, an unnamed “eminent physicist,” complained to him that physicists tended to use the Gaussian curve because they thought mathematicians believed it a mathematical necessity; mathematicians used it because they believed that physicists found it to be an empirical fact.

Eliminating Unfair Influence

Let me state here that, except for the grocery-store mentality, I truly believe in the value of middleness and mediocrity—what humanist does not want to minimize the discrepancy between humans? Nothing is more repugnant than the inconsiderate ideal of the Übermensch! My true problem is epistemological. Reality is not Mediocristan, so we should learn to live with it.

“The Greeks Would Have Deified It”

The list of people walking around with the bell curve stuck in their heads, thanks to its Platonic purity, is incredibly long.

Sir Francis Galton, Charles Darwin’s first cousin and Erasmus Darwin’s grandson, was perhaps, along with his cousin, one of the last independent gentlemen scientists—a category that also included Lord Cavendish, Lord Kelvin, Ludwig Wittgenstein (in his own way), and to some extent, our überphilosopher Bertrand Russell. Although John Maynard Keynes was not quite in that category, his thinking epitomizes it. Galton lived in the Victorian era when heirs and persons of leisure could, among other choices, such as horseback riding or hunting, become thinkers, scientists, or (for those less gifted) politicians. There is much to be wistful about in that era: the authenticity of someone doing science for science’s sake, without direct career motivations.

Unfortunately, doing science for the love of knowledge does not necessarily mean you will head in the right direction. Upon encountering and absorbing the “normal” distribution, Galton fell in love with it. He was said to have exclaimed that if the Greeks had known about it, they would have deified it. His enthusiasm may have contributed to the prevalence of the use of the Gaussian.

Galton was blessed with no mathematical baggage, but he had a rare obsession with measurement. He did not know about the law of large numbers, but rediscovered it from the data itself. He built the quincunx, a pinball machine that shows the development of the bell curve—on which, more in a few paragraphs. True, Galton applied the bell curve to areas like genetics and heredity, in which its use was justified. But his enthusiasm helped thrust nascent statistical methods into social issues.

“Yes/No” Only Please

Let me discuss here the extent of the damage. If you’re dealing with qualitative inference, such as in psychology or medicine, looking for yes/no answers to which magnitudes don’t apply, then you can assume you’re in Mediocristan without serious problems. The impact of the improbable cannot be too large. You have cancer or you don’t, you are pregnant or you are not, et cetera. Degrees of deadness or pregnancy are not relevant (unless you are dealing with epidemics). But if you are dealing with aggregates, where magnitudes do matter, such as income, your wealth, return on a portfolio, or book sales, then you will have a problem and get the wrong distribution if you use the Gaussian, as it does not belong there. One single number can disrupt all your averages; one single loss can eradicate a century of profits. You can no longer say “this is an exception.” The statement “Well, I can lose money” is not informational unless you can attach a quantity to that loss. You can lose all your net worth or you can lose a fraction of your daily income; there is a difference.

This explains why empirical psychology and its insights on human nature, which I presented in the earlier parts of this book, are robust to the mistake of using the bell curve; they are also lucky, since most of their variables allow for the application of conventional Gaussian statistics. When measuring how many people in a sample have a bias, or make a mistake, these studies generally elicit a yes/no type of result. No single observation, by itself, can disrupt their overall findings.

I will next proceed to a sui generis presentation of the bell-curve idea from the ground up.

A (LITERARY) THOUGHT EXPERIMENT ON WHERE THE BELL CURVE COMES FROM

Consider a pinball machine like the one shown in Figure 8. Launch 32 balls, assuming a well-balanced board so that the ball has equal odds of falling right or left at any juncture when hitting a pin. Your expected outcome is that many balls will land in the center columns and that the number of balls will decrease as you move to the columns away from the center.

Next, consider a gedanken, a thought experiment. A man flips a coin and after each toss he takes a step to the left or a step to the right, depending on whether the coin came up heads or tails. This is called the random walk, but it does not necessarily concern itself with walking. You could identically say that instead of taking a step to the left or to the right, you would win or lose $1 at every turn, and you will keep track of the cumulative amount that you have in your pocket.

Assume that I set you up in a (legal) wager where the odds are neither in your favor nor against you. Flip a coin. Heads, you make $1, tails, you lose $1.

At the first flip, you will either win or lose.

At the second flip, the number of possible outcomes doubles. Case one: win, win. Case two: win, lose. Case three: lose, win. Case four: lose, lose. Each of these cases has equivalent odds, the combination of a single win and a single loss has an incidence twice as high because cases two and three, win-lose and lose-win, amount to the same outcome. And that is the key for the Gaussian. So much in the middle washes out—and we will see that there is a lot in the middle. So, if you are playing for $1 a round, after two rounds you have a 25 percent chance of making or losing $2, but a 50 percent chance of breaking even.

FIGURE 8: THE QUINCUNX (SIMPLIFIED)—A PINBALL MACHINE

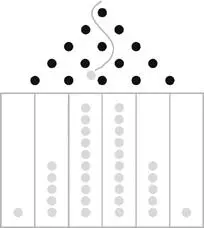
Drop balls that, at every pin, randomly fall right or left. Above Is the most probable scenario, which greatly resembles the bell curve (a.k.a. Gaussian disribution). Courtesy of Alexander Taleb .

Let us do another round. The third flip again doubles the number of cases, so we face eight possible outcomes. Case 1 (it was win, win in the second flip) branches out into win, win, win and win, win, lose. We add a win or lose to the end of each of the previous results. Case 2 branches out into win, lose, win and win, lose, lose. Case 3 branches out into lose, win, win and lose, win, lose. Case 4 branches out into lose, lose, win and lose, lose, lose.

We now have eight cases, all equally likely. Note that again you can group the middling outcomes where a win cancels out a loss. (In Galton’s quincunx, situations where the ball falls left and then falls right, or vice versa, dominate so you end up with plenty in the middle.) The net, or cumulative, is the following: 1) three wins; 2) two wins, one loss, net one win; 3) two wins, one loss, net one win; 4) one win, two losses, net one loss; 5) two wins, one loss, net one win; 6) two losses, one win, net one loss; 7) two losses, one win, net one loss; and, finally, 8) three losses .

Out of the eight cases, the case of three wins occurs once. The case of three losses occurs once. The case of one net loss (one win, two losses) occurs three times. The case of one net win (one loss, two wins) occurs three times.