Нассим Талеб - The Black Swan. The Impact of the Highly Improbable

Note that I am not telling you that the Mediocristan type of randomness does not allow for some extremes. But it tells you that they are so rare that they do not play a significant role in the total. The effect of such extremes is pitifully small and decreases as your population gets larger.

To be a little bit more technical here, if you have an assortment of giants and dwarfs, that is, observations several orders of magnitude apart, you could still be in Mediocristan. How? Assume you have a sample of one thousand people, with a large spectrum running from the dwarf to the giant. You are likely to see many giants in your sample, not a rare occasional one. Your average will not be impacted by the occasional additional giant because some of these giants are expected to be part of your sample, and your average is likely to be high. In other words, the largest observation cannot be too far away from the average. The average will always contain both kinds, giants and dwarves, so that neither should be too rare—unless you get a megagiant or a microdwarf on very rare occasion. This would be Mediocristan with a large unit of deviation.

Note once again the following principle: the rarer the event, the higher the error in our estimation of its probability—even when using the Gaussian.

Let me show you how the Gaussian bell curve sucks randomness out of life—which is why it is popular. We like it because it allows certainties! How? Through averaging, as I will discuss next.

How Coffee Drinking Can Be Safe

Recall from the Mediocristan discussion in Chapter 3 that no single observation will impact your total. This property will be more and more significant as your population increases in size. The averages will become more and more stable, to the point where all samples will look alike.

I’ve had plenty of cups of coffee in my life (it’s my principal addiction). I have never seen a cup jump two feet from my desk, nor has coffee spilled spontaneously on this manuscript without intervention (even in Russia). Indeed, it will take more than a mild coffee addiction to witness such an event; it would require more lifetimes than is perhaps conceivable—the odds are so small, one in so many zeroes, that it would be impossible for me to write them down in my free time.

Yet physical reality makes it possible for my coffee cup to jump—very unlikely, but possible. Particles jump around all the time. How come the coffee cup, itself composed of jumping particles, does not? The reason is, simply, that for the cup to jump would require that all of the particles jump in the same direction, and do so in lockstep several times in a row (with a compensating move of the table in the opposite direction). All several trillion particles in my coffee cup are not going to jump in the same direction; this is not going to happen in the lifetime of this universe. So I can safely put the coffee cup on the edge of my writing table and worry about more serious sources of uncertainty.

FIGURE 7: How the Law of Large Numbers Works

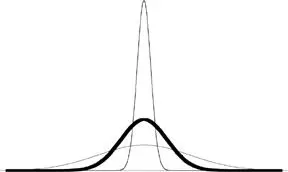
In Mediocristan, as your sample size increases, the observed average will present itself with less and less dispersion—as you can see, the distribution will be narrower and narrower. This, in a nutshell, is how everything in statistical theory works (or is supposed to work). Uncertainty in Mediocristan vanishes under averaging. This illustrates the hackneyed “law of large numbers.”

The safety of my coffee cup illustrates how the randomness of the Gaussian is tamable by averaging. If my cup were one large particle, or acted as one, then its jumping would be a problem. But my cup is the sum of trillions of very small particles.

Casino operators understand this well, which is why they never (if they do things right) lose money. They simply do not let one gambler make a massive bet, instead preferring to have plenty of gamblers make series of bets of limited size. Gamblers may bet a total of $20 million, but you needn’t worry about the casino’s health: the bets run, say, $20 on average; the casino caps the bets at a maximum that will allow the casino owners to sleep at night. So the variations in the casino’s returns are going to be ridiculously small, no matter the total gambling activity. You will not see anyone leaving the casino with $1 billion—in the lifetime of this universe.

The above is an application of the supreme law of Mediocristan: when you have plenty of gamblers, no single gambler will impact the total more than minutely.

The consequence of this is that variations around the average of the Gaussian, also called “errors,” are not truly worrisome. They are small and they wash out. They are domesticated fluctuations around the mean.

Love of Certainties

If you ever took a (dull) statistics class in college, did not understand much of what the professor was excited about, and wondered what “standard deviation” meant, there is nothing to worry about. The notion of standard deviation is meaningless outside of Mediocristan. Clearly it would have been more beneficial, and certainly more entertaining, to have taken classes in the neurobiology of aesthetics or postcolonial African dance, and this is easy to see empirically.

Standard deviations do not exist outside the Gaussian, or if they do exist they do not matter and do not explain much. But it gets worse. The Gaussian family (which includes various friends and relatives, such as the Poisson law) are the only class of distributions that the standard deviation (and the average) is sufficient to describe. You need nothing else. The bell curve satisfies the reductionism of the deluded.

There are other notions that have little or no significance outside of the Gaussian: correlation and, worse, regression . Yet they are deeply ingrained in our methods; it is hard to have a business conversation without hearing the word correlation .

To see how meaningless correlation can be outside of Mediocristan, take a historical series involving two variables that are patently from Extremistan, such as the bond and the stock markets, or two securities prices, or two variables like, say, changes in book sales of children’s books in the United States, and fertilizer production in China; or real-estate prices in New York City and returns of the Mongolian stock market. Measure correlation between the pairs of variables in different subperiods, say, for 1994, 1995, 1996, etc. The correlation measure will be likely to exhibit severe instability; it will depend on the period for which it was computed. Yet people talk about correlation as if it were something real, making it tangible, investing it with a physical property, reifying it.

The same illusion of concreteness affects what we call “standard” deviations. Take any series of historical prices or values. Break it up into subsegments and measure its “standard” deviation. Surprised? Every sample will yield a different “standard” deviation. Then why do people talk about standard deviations? Go figure.

Note here that, as with the narrative fallacy, when you look at past data and compute one single correlation or standard deviation, you do not notice such instability.

How to Cause Catastrophes

If you use the term statistically significant , beware of the illusions of certainties. Odds are that someone has looked at his observation errors and assumed that they were Gaussian, which necessitates a Gaussian context, namely, Mediocristan, for it to be acceptable.