Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

2. Свойство диагоналей прямоугольника.

3. На сторонах угла Q отложены равные отрезки QR и QP. Через точки R и P проведена прямая. Определите ?QRP, если ?RPQ = 67°.

4. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна его основанию.

1. Формула длины окружности (формула и пример).

2. Первый признак равенства треугольников.

3. Найдите площадь квадрата, если его диагональ равна 5 см.

4. Сколько сторон имеет выпуклый многоугольник, у которого все углы равны, если сумма его внешних углов с одним из внутренних равна 468°?

1. Формулы площади треугольника (формулы и примеры).

2. Признаки параллелограмма.

3. Докажите, что общая хорда двух пересекающихся окружностей перпендикулярна линии центров.

4. Средняя линия описанной около окружности трапеции равна 4. Найдите периметр трапеции.

1. Формулы площади прямоугольника и параллелограмма (формулы и примеры).

2. Второй признак равенства треугольников.

3. На сколько увеличится или уменьшится длина окружности, если ее радиус увеличить на 10 см.

4. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба.

1. Формула площади трапеции (формула и пример).

2. Признаки равенства прямоугольных треугольников.

3. Даны точки А (1, -3) и В (2, 0). Найдите такую точку С (х, у), чтобы векторы АВ и СА были равны.

4. Точка касания окружности, вписанной в равнобедренный треугольник, делит боковую сторону на отрезки, равные 3 см и 4 см, считая от основания. Найдите периметр треугольника.

1. Формула площади круга (формула и пример).

2. Теорема Пифагора.

3. Докажите, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию.

4. Найдите геометрическое место середин равных хорд окружности.

1. Равенство фигур. Признаки равенства треугольников (доказательство одного из них).

2. Критерий описанного около окружности четырёхугольника (без доказательства).

3. Точка С – середина отрезка АВ. Найдите длину отрезка АС в дециметрах, если АВ = 7 м 58 см.

4. В прямоугольнике ABCD AD = 12 см, CD = 5 см, О – точка пересечения диагоналей. Найдите

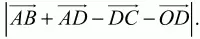
5. В треугольнике ABC угол А = углу В = 75°. Найдите ВС, если площадь треугольника равна 36 см2.

1. Сумма углов треугольника (с доказательством). Вывод формулы суммы углов выпуклого n-угольника.

2. Критерий вписанного в окружность четырёхугольника (без доказательства).

3. Основания трапеции относятся как 2:3, а высота равна 6 см. площадь трапеции 60 см2. Найдите основания трапеции.

4. В прямоугольном треугольнике ABC АВ = 6 см, АС = 8 см. ВС = 10 см. Найдите расстояние:

а) от точки В до прямой АС;

б) от точки С до прямой АВ.

Может ли расстояние от точки А до прямой СВ быть равным 7 см?

5. Точка М принадлежит отрезку РК, причем РМ: МК = 2:1. Найдите координаты точки К, если координаты точек Р и М равны (6; 3) и (14; 9) соответственно.

1. Геометрическое место центров описанной около треугольника и вписанной в треугольник окружностей (с доказательством).

2. Площадь четырёхугольника (без вывода).

3. Даны треугольник ABC и точка М на отрезке ВС. Выразите:

а) вектор СВ через векторы АС и АВ;

б) вектор МА через векторы ВА и ВМ.

4. В ромбе ABCD, где угол А острый, BE и BF – высоты. Угол между диагональю BD и высотой BF равен 40°:

а) докажите, что BE = BF.

б) найдите углы ромба.

5. В треугольнике ABC точки F и М лежат соответственно на сторонах АВ и ВС, причем CF = AM, а угол MAC = углу FCA. Докажите, что треугольник ABC равнобедренный.

1. Свойства параллелограмма (с доказательством).

2. Геометрическое введение синуса, косинуса, тангенса котангенса. Значения sin, cos, tg, ctg от углов 30°, 45°, 60°.

3. Прямой угол ADB разделен лучом DC на два угла, из которых один больше другого на 8°. Найдите градусные меры этих углов.

4. В равнобедренной трапеции ABCD угол А = 30°, угол ACD = 135°, AD = 20 см, ВС = 10 см:

а) докажите, что АС – биссектриса угла ВАС;

б) найдите периметр трапеции.

5. В треугольнике ABC АВ = 17 см, ВС = 25 см. Высота BD равна 15 см. Найдите площадь треугольника.