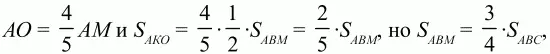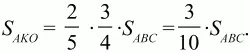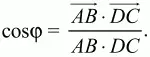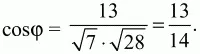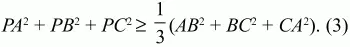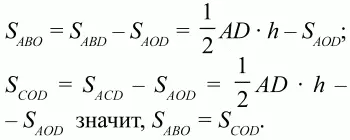Итак,
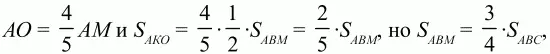
значит,
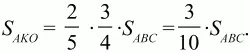
Ответ: 3/10.
153. В выпуклом четырёхугольнике ABCD диагонали АС и BD пересекаются в точке F. Известно, что AF = CF = 2, BF = 1, DF = 4, ?BFC = ?/3.
Найти косинус угла между векторами АВ и DC (рис. 208). (3)
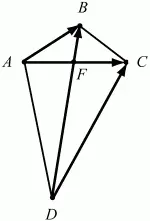
Рис. 208.
Решение:
Пусть ? – искомый угол между векторами АВ и DC тогда
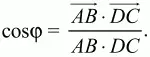
Пользуясь свойствами скалярного произведения векторов и условиями задачи, вычислим АВ, DC и АВ ? DC. Так как

Теперь получаем, что
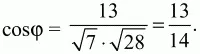
Ответ: 13/14.
Задачи для самостоятельного решения
154. Найдите геометрическое место точек, равноудалённых от данной прямой и данной точки. (2)
155. Продолжения сторон AD и ВС четырёхугольника ABCD пересекаются в точке Р. Точки М и N – середины сторон АВ и CD. Доказать, что если прямая MN проходит через точку Р, то ABCD – трапеция. (3)
156. Дан равнобедренный треугольник ABC, в котором проведены высота CD и перпендикуляр DE к боковой стороне ВС. Точка M – середина отрезка DE. Доказать, что отрезки АЕ и СМ перпендикулярны. (3)
157. Доказать, что для треугольника ABC и любой точки Р выполняется неравенство:
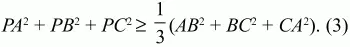
Примеры решения задач
158. Можно ли утверждать, что треугольники равны по двум сторонам и медиане, проведенной к одной из этих сторон? Ответ: обоснуйте (рис. 209). (1)
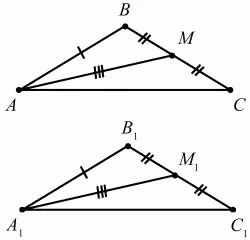
Рис. 209.
Решение. Рассмотрим треугольники ABC и А1В1C1. Пусть AB = A1B1, BC = B1C1,AM = A1M1 (см. рис). Так как ВС = В1С1, то ВМ = В1М1 ?АВМ = ?A1B1M1 (по трём сторонам), значит, ?В = ?B1. В этом случае ?ABC = ?A1B1C1 по двум сторонам и углу между ними.
Ответ: да.
159. Определите острые углы прямоугольного треугольника, если медиана, проведённая к его гипотенузе, делит прямой угол в отношении 2:1 (рис. 210). (1)
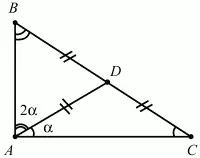
Рис. 210.
Решение. Нарисуем треугольник ABC, где ?ВАС = 3? = 90°. Медиана AD равна длинам BD и CD, так как D – середина гипотенузы, а, значит, является центром описанной около треугольника окружности. Пусть для определённости ?BAD = 2?, ?DAC =?. Очевидно, что 2? + ? = 90°, ? = 30°. Учитывая, что треугольники BDA и DAC – равнобедренные, получаем:?В = 2? = 60°, ?С = ? = 30°.
Ответ: 60°, 30°.
160. Дан произвольный четырёхугольник ABCD. Точки М, N, Р, Q – середины его сторон. Докажите, что MNPQ – параллелограмм (рис. 211). (1)
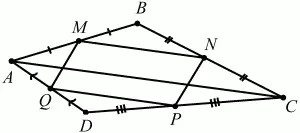
Рис. 211.
Решение. Из условия задачи и чертежа видно, что MN – средняя средняя линия ?ABC и QP средняя линия ?ACD. Поэтому MN = 1/2АС и MN||AC; QP = 1/2АС и QP||АС. В итоге получаем, что MN = QP и MN||QP. Поэтому, по признаку параллелограмма четырёхугольник MNPQ – параллелограмм.
161. Диагонали АС и BD трапеции ABCD пересекаются в точке О. Докажите, что треугольник АОВ и COD имеют одинаковые площади (рис. 212). (2)
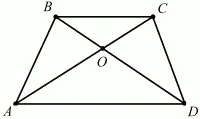
Рис. 212.
Решение. Обозначим через h высоту трапеции. Запишем равенства:
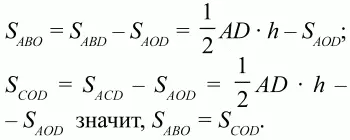
162. Стороны треугольника образуют арифметическую прогрессию. Доказать, что радиус окружности, вписанной в треугольник, равен 1/3 высоты, проведённой к средней по величине стороне треугольника. (3)
Решение. Пусть стороны а, b, с треугольника ABC образуют арифметическую прогрессию с разностью d. Будем считать, что а ? b ? с. тогда a = b – d, c = b + d, периметр Р = 2р = 3b.
Воспользуемся формулой r = S/P, получим r = 2S/3b. А так как S = 1/2bhb, то r = 1/3hb.
Задачи для самостоятельного решения
163. Диагонали трапеции делят её среднюю линию на три равные части. Как относятся основания этой трапеции? (1)
Читать дальше
Конец ознакомительного отрывка
Купить книгу