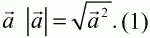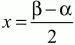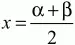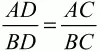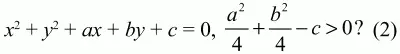Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

32. Докажите, что медиана треугольника ABC, проведённая из вершины А, меньше полусуммы сторон АВ и АС. (1)

33. Могут ли пересекаться окружности с радиусами R1 и R2 и расстоянием между центрами d, если R1 + R2 < d? (1)

34. Найдите радиус r окружности, вписанной в равносторонний треугольник со стороной а, и радиус R окружности, описанной около него. (1)

35. Найдите геометрическое место точек плоскости ху, для которых |х| = 3. (1)

36. Составьте уравнение окружности с центром в точке (1; 2), касающейся оси х. (1)

37. Докажите, что прямая, содержащая медиану равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника. (1)

38. Сколько осей симметрии у равностороннего треугольника? (1)

39. Докажите, что ромбы равны, если у них равны диагонали. (1)

40. Даны точки A(0; 1), В(1; 0), С(1; 2), D(2; 1). Докажите равенство векторов АВ и CD.(1)

41. Дан параллелограмм ABCD, AC = a, DB = b. Выразите векторы АВ, СВ, CD и АD через а и b (рис. 117).(1)

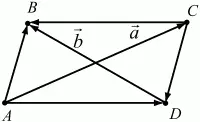
Рис. 117.

42. Докажите, что для любого вектора

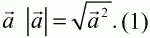
43. Докажите, что дуги окружности, заключённые между параллельными хордами, равны. (2)

44. Докажите правильность соотношения

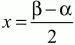
(рис. 118). (2)

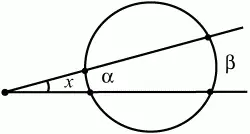
Рис. 118.

45. Докажите правильность соотношения

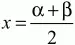
(рис. 119). (2)

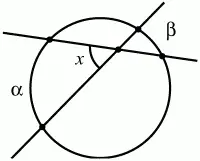
Рис. 119.

46. АВ – касательная. Докажите, что х = ?/2 (рис. 120). (2)

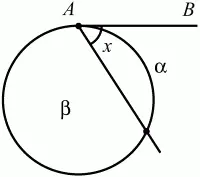
Рис. 120.

47. Докажите, что если два треугольника подобны с коэффициентом подобия k, то с тем же коэффициентом подобия подобны соответствующие линейные элементы этих треугольников (высоты, медианы, радиусы описанной и вписанной окружностей, периметры и т. д.). (2)

48. Докажите, что если для четырёх точек плоскости А, В, М и К выполняется одно из следующих условий: а) точки М и К расположены по одну сторону от прямой АВ и при этом ?АМВ = ?АКБ; б) точки М и К расположены по разные стороны от прямой АВ и при этом ?АМВ + ?АКБ = 180°, то точки А, В, М и К лежат на одной окружности. (2)

49. Докажите, что биссектриса внешнего угла треугольника обладает свойством, аналогичному биссектрисе внутреннего угла, а именно:

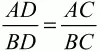
(рис. 121). (2)

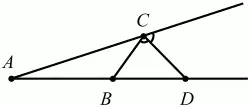
Рис. 121.

50. ABC – произвольный треугольник. СР и AQ – высоты. Докажите, что треугольник ABC и треугольник PBQ подобны. Чему равен коэффициент подобия (рис. 122)? (2)

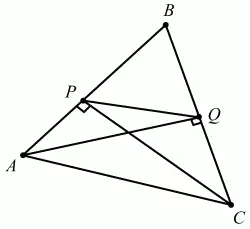
Рис. 122.

51. Докажите равенство треугольников по медиане и углам, на которые медиана разбивает угол треугольника. (2)

52. Докажите равенство треугольников по стороне, медиане, проведённой к этой стороне, и углам, которые образует с ней медиана. (2)

53. Разделите отрезок АВ с помощью циркуля и линейки на n равных частей. (2)

54. На стороне АВ треугольника ABC взята точка X Докажите, что отрезок СХ меньше, по крайней мере, одной из сторон АС или ВС. (2)

55. Какая геометрическая фигура задана уравнением

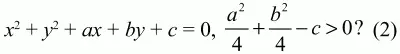
56. Докажите, что при движении параллелограмм переходит в параллелограмм. (2)

57. Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии. (2)

58. Докажите, что отрезки, соединяющие противоположные вершины описанного шестиугольника, пересекаются в одной точке (теорема Брианшона). (3)

59. Докажите, что основания перпендикуляров, проведённых к прямым, содержащим стороны треугольника, из произвольной точки описанной около него окружности, лежат на одной прямой (теорема Симпсона). (3)

60. Докажите, что если противоположные стороны вписанного шестиугольника не параллельны, то точки пересечения продолжений этих сторон лежат на одной прямой (теорема Паскаля). (3)