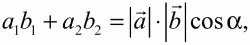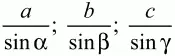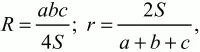Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

37. Даны векторы а = (а1; а2) и b = (BL; b2). Докажите, что

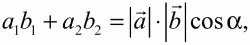
где ? – угол между векторами.

38. а) Какие вы знаете свойства скалярного произведения векторов? (1)

б) Докажите эти свойства. (2)

39. Докажите, что гомотетия есть преобразование подобия. (1)

40. а) Какие вы знаете свойства преобразования подобия? (1)

б) Докажите, что преобразование подобия сохраняет углы между лучами. (2)

41. а) Сформулируйте признак подобия треугольников по двум углам. (1)

б) Докажите этот признак. (1)

42. а) Сформулируйте признак подобия треугольников по двум сторонам и углу между ними. (1)

б) Докажите этот признак. (1)

43. а) Сформулируйте признак подобия треугольников по трём сторонам. (1)

б) Докажите этот признак. (2)

44. а) Сформулируйте свойство биссектрисы треугольника. (1)

б) Докажите, что биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. (1)

45. а) Сформулируйте свойство вписанного в окружность угла. (1)

б) Докажите это свойство. (1)

46. а) Докажите, что если хорды АВ и CD окружности пересекаются в точке S, то AS ? BS = CS ? DS. (1)

б) Докажите, что если из точки S к окружности проведены две секущие, пересекающие окружность в точках А, В и С, D соответственно, то AS ? BS = CS ? DS. (1)

47. а) Сформулируйте теорему косинусов для треугольника. (1)

б) Докажите эту теорему. (1)

48. а) Сформулируйте теорему синусов. (1)

б) Докажите эту теорему. (1)

в) Докажите, что в теореме синусов каждое из трёх отношений:

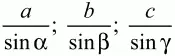
равно 2R, где R – радиус описанной около треугольника окружности. (1)

49. Докажите, что в треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона. (2)

50. а) Чему равна сумма углов выпуклого n-угольника? (1)

б) Выведите формулу суммы углов выпуклого n-угольника. (1)

51. а) Докажите, что в правильный многоугольник можно вписать окружность. (1)

б) Докажите, что около правильного многоугольника можно описать окружность. (1)

52. Дан правильный n-угольник со стороной а. Выведите формулы:

а) радиусов вписанной и описанной окружностей; (1)

б) площади n-угольника; (1)

в) угла при вершине. (1)

53. Докажите, что отношение длины окружности к её диаметру не зависит от размера окружности. (3)

54. Как переводить углы из градусной меры в радианную и наоборот? (1)

55. Докажите, что площадь прямоугольника равна произведению длины прямоугольника на его ширину. (3)

56. а) По какой формуле вычисляется площадь параллелограмма? (1)

б) Выведите эту формулу. (1)

57. а) По какой формуле вычисляется площадь треугольника? (через основание и высоту). (1)

б) Выведите эту формулу. (1)

в) Выведите формулу Герона. (1)

58. а) По какой формуле вычисляется площадь трапеции? (1)

б) Выведите эту формулу. (1)

59. Выведите формулы:

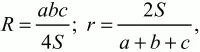
где a, b, c – длины сторон треугольника;

S – его площадь;

R и r – радиусы описанной и вписанной окружностей. (1)

60. Пусть F1 и F2 – две подобные фигуры с коэффициентом подобия k. Как относятся площади этих фигур? Ответ: обоснуйте. (1)

61. а) По какой формуле вычисляется площадь круга? (1)

б) Выведите эту формулу. (3)

62. Выведите формулу площади кругового сектора. (2)

63. Выведите формулу площади кругового сегмента. (2)

64. а) Докажите, что биссектрисы треугольника пересекаются в одной точке. (2)

б) Докажите, что медианы треугольника пересекаются в одной точке. (2)

в) Докажите, что высоты треугольника (или их продолжения) пересекаются в одной точке. (2)

г) Докажите, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. (1)

65. Докажите, что площадь треугольника равна половине произведения двух его сторон на синус угла между ними. (1)

66. а) Сформулируйте теорему Чевы. (3)

б) Докажите эту теорему. (3)

в) Сформулируйте и докажите обратную теорему. (3)

67. а) Сформулируйте теорему Мене лая. (3)

б) Докажите эту теорему. (3)

в) Сформулируйте и докажите обратную теорему. (3)

68. а) Докажите, что если стороны одного угла параллельны сторонам другого угла, то такие углы либо равны, либо составляют 180°. (2)

б) Докажите, что если стороны одного угла перпендикулярны сторонам другого угла, то такие углы равны или составляют 180°. (2)