Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

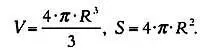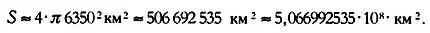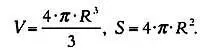
Если радиус Земли взять равным примерно 6350 км, тогда общая площадь Земли составит:

* * *

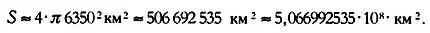
ГРАДУСЫ И РАДИАНЫ

Радиан определяется как величина центрального угла окружности, длина дуги которого равна радиусу окружности. Эта величина составляет примерно 55 градусов 17 минут и 44 секунды. Радиан (часто обозначаемый как рад, rad ) используется в качестве единицы измерения так называемой «круговой меры угла». Если круговая мера угла в радианах равна а , то угол будет равен 180°· а/ πградусов, и наоборот если угол равен G ° , то круговая мера угла составит π· G/ 180радиан.

То есть угол в 360° полной окружности составит 2· πрадиан. В общем случае эти вычисления осуществляются следующим образом.

Если πрадиан соответствует 180°, то Rрадиан соответствует G ° , что дает нам следующую пропорцию: π/ 180 = R/ G. Например, сколько радиан имеет угол в 30°? Подставляя в формулу, получим π/ 180 = R/ 30, откуда находим R:

R= (30· π/180 )= π/6 рад.

Мы также можем решить обратную задачу. Сколько градусов имеет угол в π/4 радиан? Подставляя в формулу, получим

π/180 = ( π/4)/ G, откуда находим G:

G= (( π/4)·180)/ π= 45°

* * *

Применим теперь формулу для объема и получим:

V= (4· π·6350 3)/3 = 1,072499199·10 12·км 3

С этими результатами мы можем вычислить площадь октанта, одной восьмой части земной поверхности. Просто разделим значение площади Земли на 8. Это дает нам 63336566,88 км 2.

Как мы видим, каждый октант очерчивает сферический треугольник с углами 90° = π/2 радиан. Обратите внимание, что общая сумма составляет 270° = З π/2 радиан (то есть более чем 180° = πрадиан). Тогда чему будет равна каждая из сторон?

Каждая из сторон представляет собой дугу большого круга. Используя формулу для длины дуги, получим:

( α· R) = ( π/2)·6350 = 9 974,2625 км

Этот же результат можно получить и другим способом: разделить длину большого круга на четыре (напомним, что длина окружности составляет 2πR):

( 2π·6350)/4 = 9974,2625 км.

Ясно, что ту же процедуру можно повторить для Луны, радиус которой равен 1736 км.

* * *

ДЛИНА ДУГИ КРУГОВОГО СЕКТОРА

Для части окружности с центром O и радиусом r , изображенной на рисунке, обозначим α угол, измеряемый, как правило, в радианах, а с — дугу между точками А и B . Тогда длина дуги выражается следующим образом: с= α· r.

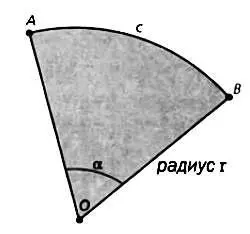
Имея дело с длиной стороны сферического треугольника, мы обычно используем круговую меру угла, которую фактически нужно лишь умножить на радиус.

* * *

Вернемся к нашему общему вопросу. Геодезической линией называется кратчайшая линия, соединяющая две точки на поверхности и сама принадлежащая этой поверхности. На совершенно плоской, то есть евклидовой поверхности, геодезической линией является отрезок. Между двумя точками А и В на сферической поверхности из всех окружностей, проходящих через эти точки и расположенных на этой сфере, геодезической линией является большой круг. Другими словами, геодезическая линия получается путем пересечения сферы плоскостью АОВ . Таким образом, геодезическим отрезком между точками А и В является меньшая из дуг большого круга, проходящего через А и В . Обратите внимание, что случай с этим кругом — единственный, когда А и В не являются диаметрально противоположными точками.

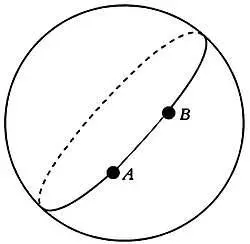
В геометрии на сфере прямыми линиями являются дуги больших кругов. Таким образом, параллельные линии не существуют, так как большие круги всегда пересекаются в диаметрально противоположных точках. Для наглядности достаточно взглянуть на дольки очищенного апельсина.

* * *