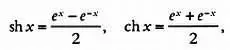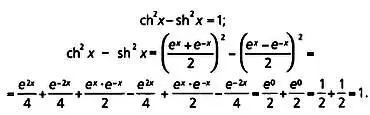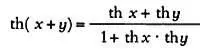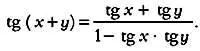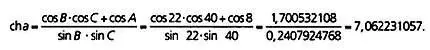Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

Для переменной х гиперболический синус и гиперболический косинус определяются следующим образом:

Аналогично элементарной тригонометрии, гиперболический тангенс определяется следующей формулой:

th x = sh x / ch x

Здесь мы вкратце напомним так называемую теорему синусов.

В треугольнике со сторонами а, b и с и с углами А, В и С

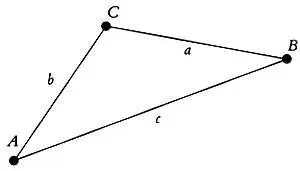
справедливо следующее соотношение:

a / sin A = b / sin В = c / sin С

Аналогичное соотношение можно сформулировать в гиперболической тригонометрии:

sin A / sh a = sin B / sh b = sin С / sh c

Чтобы проверить гиперболические равенства, нужно подставить вместо гиперболических функций их определения:

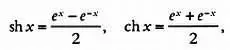
и затем, выполнив соответствующие расчеты, убедиться, что получится один и тот же ответ.

Используя определения гиперболических синуса и косинуса, можно вывести и другие тригонометрические тождества, аналогичные известным тождествам из евклидовой геометрии. Например, мы можем проверить, что

ch(x + у) = chx· chy + shx· shy

аналогично традиционному выражению

cos(x + у) = cosx· cosy + sinx· siny

* * *

ОСНОВНОЕ ТОЖДЕСТВО ГИПЕРБОЛИЧЕСКОЙ ТРИГОНОМЕТРИИ

В евклидовой тригонометрии есть важное соотношение, называемое основным тригонометрическим тождеством, которое утверждает, что sin 2x + cos 2x = 1. Аналогом в гиперболической тригонометрии является следующее тождество:

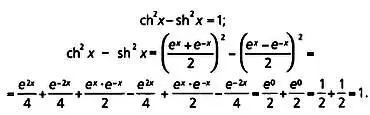
ВОПРОС ТЕРМИНОЛОГИИ

В евклидовой терминологии синус и косинус называются круговыми функциями, поскольку они получаются из свойств круга. Рассмотрим окружность радиуса 1 с центром в начале системы координат. Уравнение этой окружности записывается как х 2+ у 2= 1. В этом простом уравнении мы можем сделать замену переменной, выразив переменные х и у через параметр t следующим образом: х = cost и у = sint. Здесь х и у удовлетворяют соотношению х 2+ у 2= 1. Такое уравнение называется параметрическим уравнением окружности.

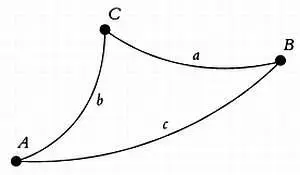
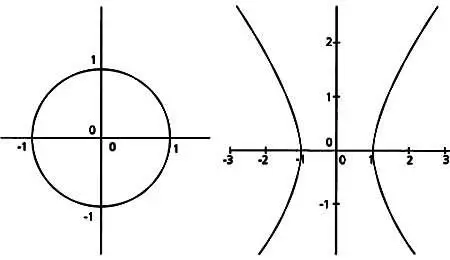
Если вместо круга мы возьмем гиперболу, график функции х 2— у 2 = 1, то х = cht и у = sht удовлетворяют соотношению х 2 — у 2 = 1. Это уравнение называется «уравнением гиперболы».

Эти графики нам уже знакомы. Гипербола напоминает нам псевдосферу.

* * *

Что касается тангенсов, то можно показать, что

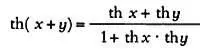
аналогично традиционному выражению

* * *

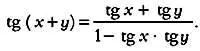
ЕВКЛИДОВА ТРИГОНОМЕТРИЯ

Тригонометрические тождества для суммы и разности выглядят следующим образом:

sin(x + у) = sinx· cosy + cosx· siny

cos(x + у) = cosx· cosy — sinx· siny

sin(x — y) = sinx· cosy — cosx· siny

cos(x — y ) = cosx· cosy + sinx· siny

* * *

РЕШЕНИЕ ГИПЕРБОЛИЧЕСКОГО ТРЕУГОЛЬНИКА ПО ЕГО УГЛАМ

Пусть в гиперболическом треугольнике даны внутренние углы А = 8°, В = 22° и С = 40°. Надо найти угловой дефект и длины сторон треугольника.

Угловой дефект считается по формуле 180° — (8° + 22° + 40°) = 110°. Для вычисления длин сторон мы воспользуемся гиперболической теоремой косинусов и получим

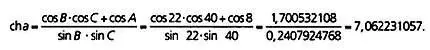
Это позволяет нам вычислить значение а . Для этого воспользуемся калькулятором и посчитаем функцию, обратную гиперболическому косинусу. Получим значение 2,642857562. Далее