Микель Альберти - Мир математики. т.20. Творчество в математике. По каким правилам ведутся игры разума

«Посадка в шахматном порядке <���…>. Чтобы определить, где следует сажать деревья, достаточно, чтобы один рабочий взял в руки рулетку и встал там, где нужно посадить первое дерево. Второй рабочий, взяв в руки конец рулетки, должен отойти на расстояние, равное желаемому расстоянию между деревьями (например, 5 м) и отмотать ленту длиной в два раза больше чем требуется (если деревья планируется посадить на расстоянии 5 м друг от друга, рабочий должен отмотать 10 м ленты рулетки). Третий рабочий должен взяться за середину ленты рулетки и отойти в сторону, натягивая ленту. Когда лента рулетки натянется полностью, третий рабочий окажется точно в том месте, где нужно посадить третье дерево».

Здесь равносторонний треугольник понимается как частный случай равнобедренного. Именно на этом примере можно оценить справедливость фразы: теоретическое решение практической задачи обычно является не лучшим практическим решением. Вот и в этом случае решение, предложенное профессиональным математиком, на практике не применяется. С математической точки зрения, напротив, практика не имеет значения. Не имеет значения и то, что в практическом решении равносторонний треугольник понимается иначе — для математика это не новость.

Тем не менее практически решил эту задачу не математик, а садовод. И практическое решение математической задачи — это результат математического творчества.

При обрезке деревьев обычно удаляются ветви нижней его трети, и лесничему нужно на глаз определить эту часть дерева. Является ли треть того, что мы видим, третьей частью того, на что мы смотрим? Как правило, это не так:

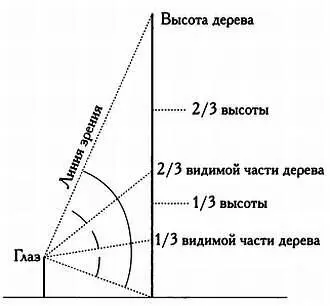
Визуальное и реальное деление предмета на три части совпадают, только когда мы рассматриваем дугу окружности, находясь в ее центре. Как же лесничий решит задачу? Как визуально определить треть предмета, на который он смотрит?

Чаще всего точная высота дерева нам неизвестна. Если А 1 — угол зрения, под которым можно увидеть все дерево, а — уровень глаз, d — расстояние до основания дерева, то угол А 3 определяющий нижнюю треть дерева, вычисляется по формуле:

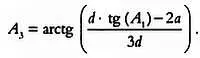
В чем заключается суть вопроса? В том, что видимая величина угла меняется в зависимости от точки, из которой мы смотрим на него. Видимая середина отрезка будет соответствовать его истинной середине только в том случае, если мы будем находиться на серединном перпендикуляре к этому отрезку:

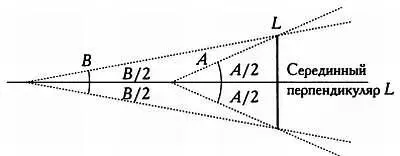
При делении отрезка на три части подобная ситуация невозможна. Если бы она была возможна, то существовала бы точка X плоскости, такая, что при взгляде из нее трети Р 1Р 2, Р 2Р 3 и P 3P 4 отрезка Р 1Р 4 были бы видны под одним и тем же углом (см. рисунок ниже). Следовательно, так как из точки X можно было бы увидеть под одним и тем же углом две половины P 1P 3 точка X должна была бы располагаться на серединном перпендикуляре к отрезку P 1P 3 (то есть на прямой, проходящей через Р 2 и перпендикулярной P 1P 3 ). Это же было бы справедливо для серединного перпендикуляра к отрезку Р 2Р 4 (прямой, проходящей через Р 3 и перпендикулярной Р 2Р 4 ). Таким образом, точка X должна была бы располагаться одновременно на двух серединных перпендикулярах, которые параллельны между собой, так как они перпендикулярны одному и тому же отрезку P 1P 4 , что невозможно:

За исключением случая, когда мы смотрим на дугу окружности, находясь в ее центре, треть того, что мы видим, — вовсе не треть того, на что мы смотрим.

Округление чисел выполняется по следующим правилам: если последний знак десятичной записи числа меньше 5, этот знак заменяется на 0, если же последний знак больше 5, то предыдущий знак увеличивается на единицу:

2,34 ~= 2,3;

2,37 ~= 2,4.

Ошибки округления в одну десятую, сотую или тысячную при работе с большими числами могут быть значительными. Если ошибка в одну сотую евро повторится на 300 миллионах счетов, общее расхождение составит 3 миллиона евро. В бухгалтерском учете подобное недопустимо. При составлении балансов даже сотые доли евро могут повлиять на итоговое значение округленной величины: