Микель Альберти - Мир математики. т.20. Творчество в математике. По каким правилам ведутся игры разума

В этой главе мы расскажем о математическом творчестве в самых разных областях, большинство из которых далеки от академической среды. Приведенные нами примеры — результат того, что кто-то задал новые вопросы, попытался найти иное решение, придать новое значение уже известным понятиям и применить уже известные идеи в новом контексте. Творчество — это жизнь. Если мы задаемся вопросами из области математики, то мы творим математику.

С чего начать? В чем секрет математического творчества? Поиски ответов на эти вопросы можно начать в повседневной жизни. Мы рассмотрим некоторые явления, с которыми сталкиваются все, но лишь немногие подошли к ним с математической точки зрения. Далее мы отойдем от реальности и в итоге окажемся в чисто математическом мире.

Для того чтобы рассмотреть интересующее нас явление, объект или процесс с точки зрения математики, нужно задать объективные вопросы, ответы на которые будут определяться не нашими предпочтениями, вкусами или соображениями удобства, а требованиями четкости и измеримости. Так будет сделан первый выбор, касающийся точки зрения, которую следует принять.

Первое, что мы делаем после пробуждения утром, — это идем в ванную, чтобы привести себя в порядок. Мы смотримся в зеркало, когда умываемся, бреемся, накладываем макияж, стрижемся. Мы смотримся в зеркало каждый день. Чего мы хотим от него? Совсем немногого: мы всего лишь хотим увидеть в нем свое лицо полностью. После завтрака и перед тем, как закрыть за собой дверь и отправиться по делам, мы мельком смотрим в зеркало, чтобы проверить, все ли в порядке. Чего мы хотим от зеркала на этот раз? Чтобы мы отразились в нем в полный рост.

Сколько раз мы совершали эти действия и сколько раз мы задавались вопросом, какие размеры должно иметь зеркало, чтобы в нем полностью отразилось наше лицо или мы сами в полный рост? Мы задаемся этим вопросом крайне редко, если вообще когда-нибудь думаем об этом. Представьте, что вы стоите перед зеркалом, в котором вы отражаетесь в полный рост. Какой должна быть минимальная высота такого зеркала? Начнем с того, что изобразим эту ситуацию на схеме с помощью точек и отрезков:

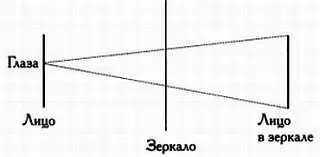
Схема показывает, какими должны быть минимальные размеры зеркала. Нужно определить, каким должно быть отношение размеров отражающей поверхности и отражающегося в ней лица. Для этого сделаем схему еще более условной: проведем вспомогательные линии, которые помогут решить задачу, и обозначим основные точки буквами:

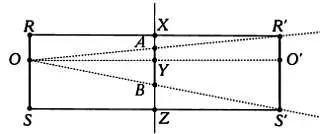
Так как отражение R'S' симметрично исходному отрезку RS , и изображение в зеркале расположено на том же расстоянии от зеркала, что и оригинал, но по другую его сторону, получим RX = XR' . Кроме того, RX = RR' /2.

Помимо этого, треугольники OAY и OR'О' подобны, так как два их угла равны. Аналогично для треугольников OYB и OO'S' . Так как RX = RR' /2, коэффициент подобия этих треугольников равен 2, поэтому AY = R'O' /2 = RO /2, а также YB = O'S' /2 = OS /2.

Иными словами, АВ = AY + YB = RO /2 + OS /2 = ( RO + OS )/2 = RS /2, так что высота зеркала должна быть равной минимум половине высоты лица. Высота, на которой следует повесить зеркало, равна BZ = YZ /2, то есть половине расстояния от глаз до подбородка. Аналогично, высота зеркала, в котором мы будем отражаться полностью, должна быть равна половине нашего роста, и такое зеркало следует повесить на высоте, равной половине расстояния от глаз до пола.

Выйдя из дома, некоторые из нас имеют счастливую возможность пойти на пляж и насладиться видом горизонта, глядя вдаль, на самый край земли, покуда хватает глаз. Кто-нибудь хоть раз, глядя на горизонт, думал о математике? Как правило, любуясь рассветом или закатом, мы задаемся другими вопросами: мы размышляем о прошлом и будущем, о красоте природы, о рыбаках, которые возвращаются из моря с дневным уловом, о том, что скрывается за линией горизонта, куда неожиданно быстро опускается горящее солнце, озаряющее наши жизни…

Но если мы посмотрим на горизонт взглядом математика, у нас возникнут совсем другие вопросы. Мы заметим, что когда мы наклоняемся, горизонт приближается, когда мы поднимаемся — горизонт отдаляется. Если мы сделаем полный оборот вокруг себя, то увидим, что горизонт круглый, поэтому мореходы в древности считали, что Земля круглая: в море, далеко от берега, они видели вокруг себя лишь круглый горизонт. Какое расстояние отделяет нас от горизонта? Каков его радиус? Какое расстояние отделяет нас от судна, которое виднеется на горизонте?