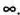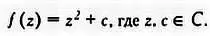Микель Альберти - Мир математики. т.20. Творчество в математике. По каким правилам ведутся игры разума

х = 0,5

f(0,5) = 0,5 2= 0,25

f(0,25) = 0,25 2= 0,0625

f(0,0625) = 0,0625 2= 0,0039

=> Орбита точки 0,5 = {0,5; 0,25; 0,0625; 0,0039; …} —> 0.

Орбита точки х = 0,5 образована убывающей ограниченной последовательностью чисел, которая стремится к 0. Существуют фиксированные орбиты, в частности для х = 0 и x = 1. Орбиты некоторых точек уходят в бесконечность, например, это справедливо для точки x = 2:

х = 2

f ( 2) = 2 2= 4

f(4) = 4 2 = 16

f(16) = 16 2= 256

=> Орбита точки 2 = {2, 4, 16, 256…} —>

Компьютер позволил увидеть, что произойдет с похожей функцией на поле комплексных чисел:

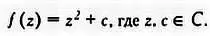
Результат оказался неожиданным и с математической, и с эстетической точки зрения, так как множества точек, не уходившие в бесконечность, принимали при различных значениях с разнообразные и удивительные формы. Эти точки образуют так называемое множество Жюлиа. Комплексные значения с , для которых множество Жюлиа является связным, то есть не разбито на несколько частей или фрагментов, образуют множество Мандельброта, которое выглядит следующим образом:

Математики смогли увидеть множество Мандельброта лишь в 1980 году, и до этого им не приходилось сталкиваться со столь же сложным объектом. Помимо фрактальной природы, ввиду которой части этого множества подобны целому, это множество обладает безграничным разнообразием. Если мы рассмотрим увеличенное изображение любой его части, то увидим, что одни и те же фигуры повторяются в нем снова и снова:

Множество М обладает самоподобием и одновременно изменчивостью бесконечной спирали. Оно являет собой прекрасный пример математического творчества.

С точки зрения топологии фрактальная кривая отличается от традиционных. Принципиальное отличие фрактальных кривых состоит как раз в их бесконечном самоподобии: если увеличить часть традиционной кривой в окрестности любой точки, она будет представлять собой отрезок, в то время как любой увеличенный фрагмент фрактальной кривой, напротив, будет иметь ту же форму, что и исходная кривая. В результате размерность фрактальных объектов не выражается целым числом от 1 до 3, в отличие от традиционных кривых. Размерность кривой Коха, например, равна 1,26186… По сути, несмотря на то что компьютер позволяет наглядно представить различные этапы построения фрактальных объектов, мы никогда не сможем увидеть результат этого процесса, так как он бесконечен. Увидеть окончательные очертания фрактальных кривых нельзя. Когда мы пытаемся поближе рассмотреть их, то видим, что они меняются и выглядят не так, как нам казалось раньше.

* * *

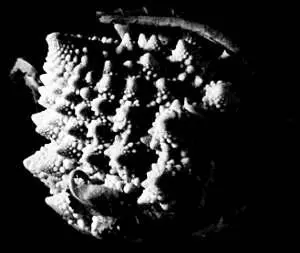
СЪЕДОБНЫЙ ФРАКТАЛ

Фракталы столь часто встречаются в реальном мире, что можно свободно говорить о фрактальной геометрии природы. Однако в природе фракталы обычно обладают не более чем четырьмя уровнями самоподобия, как, например, ветви растений, нервные окончания или подземные водоносные слои. Фрактальная размерность — это характеристика, позволяющая обнаруживать костные патологии и описывать электроэнцефалограммы.

Цветная капуста, изображенная на иллюстрации, в действительности является гибридом, который впервые был обнаружен в Италии в XVI веке. Ее структура представляет собой удивительный пример фрактальной геометрии в природе. Кочан капусты (первый уровень) состоит из уменьшенных копий самого себя (второй уровень), расположенных в форме спирали. Каждая из них, в свою очередь, также состоит из уменьшенных копий самой себя, которые вновь располагаются по спирали (третий уровень). Это же подобие наблюдается и на следующем, четвертом уровне.

В предыдущей главе мы рассказали о величайших математических творениях за всю историю математики. Сегодня эту науку двигают вперед преимущественно профессионалы, но не исключительно они. Творить математику означает не только создавать великие теоремы, которые войдут в историю, но и ставить задачи, объяснять явления с математической точки зрения, разрабатывать практические методы, позволяющие применять математику в реальной жизни, использовать технологии для развития математики, поиска математических решений и, что самое важное, понимать, когда математический ответ на заданный вопрос является необходимым и достаточным. Творить математику способны многие. Возможно, выводы, к которым они придут, не будут чем-то новым для профессиональных математиков, однако труд любителей и профессионалов по сути ничем не отличается.