Хавьер Фресан - Том. 22. Сон разума. Математическая логика и ее парадоксы

До этого момента все функции, рассмотренные в этой книге, имели единственное входное значение и преобразовывали его в другое значение посредством ряда операций. Однако в реальной жизни очень и очень немногие явления определяются всего одним параметром. Современная теория искусственных нейронных сетей, созданная на основе идей Питтса и Маккалока, позволяет имитировать работу мозга с помощью функций от нескольких параметров. Предположим, что мы хотим вычислить значение функции f , которое зависит от чисел х 1, x 2 , … х n . Основная идея здесь заключается в том, что программа, в которую передаются эти числа, обрабатывает их подобно тому, как ядро нейрона обрабатывает электрические импульсы, поступающие по отросткам. Так как величина этих импульсов может отличаться, для каждого числа х нужно указать еще одно число, ил, которое называется весом и обозначает важность каждого электрического импульса по отношению к остальным. Например, если w 1 и w n намного больше, чем w 2, w 3 … w n-1 это означает, что на результирующее значение оказывают наибольшее влияние первый и последний импульс. На основе весов импульсов в искусственной нейронной сети рассчитывается взвешенная сумма s = w 1x 1 + w 2x 2 + … + w nx n и находится значение функции, как показано на рисунке.

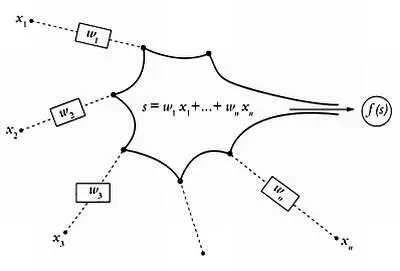
Новизна нейронных сетей заключается в том, что программа, с помощью которой мы хотим решить задачу, представляет собой не фиксированный, а открытый алгоритм, веса в котором могут изменяться. В действительности всякая нейронная сеть обычно проходит фазу обучения, на которой программа методом проб и ошибок «узнает», какие веса являются наиболее походящими, или, иными словами, какие входные сигналы следует учитывать в большей степени, чтобы итоговый результат был удовлетворительным. Если задача нашей нейронной сети заключается, например, в распознавании человеческого голоса и в ходе обучения выясняется, что большую часть первого импульса составляет фоновый шум, то сеть не будет придавать первому импульсу особого значения. Нейронные сети также очень эффективны при составлении метеорологических прогнозов и при решении задач, подобных задаче коммивояжера. Компьютеры, в которых используются нейронные сети и другие передовые алгоритмы, способны решить задачу коммивояжера уже для двухсот городов.

Благодаря нечеткой логике и нейронным сетям компьютеры, способные во многом имитировать деятельность человеческого мозга, перестали быть только частью научной фантастики. Решение новых задач стало главной целью новой, быстро развивающейся научной дисциплины — искусственного интеллекта. В течение многих лет считалось, что машина никогда не сможет играть в шахматы на уровне гроссмейстера. Вне зависимости от того, на сколько ходов вперед она способна просчитать игру, ей неизвестны слабые стороны противника, она не способна учесть иные психологические факторы. Машина не смогла бы обыграть человека и в азартные игры: как обучить компьютер игре в покер, если блеф противоречит очевидной выигрышной стратегии? Голоса критиков умолкли, когда в феврале 1996 года суперкомпьютер Deep Blue , ставший результатом работы компании IBM, начатой еще в 1950-е годы, обыграл Гарри Каспарова в первой партии шахматного матча. Затем, несмотря на то что Deep Blue мог оценивать сто миллионов позиций в секунду, из пяти следующих партий, которые игрались медленнее обычного, в четырех победу одержал российский шахматист. Однако годом позже машина была усовершенствована, и Deep Blue удалось одержать победу в трех партиях и еще одну — свести вничью, совершая ходы с той же скоростью, что и профессиональные шахматисты. Чемпион мира был повержен, однако это не помешало Каспарову по-прежнему отстаивать превосходство человека над машиной. Любопытно, что он приводил точно те же доводы, что и его противники, создавшие Deep Blue: «Это синтез, способность сочетать творчество и расчет, искусство и науку в единое целое, большее, чем сумма его частей».

Гарри Каспаровобдумывает очередной ход в партии против суперкомпьютера Deep Blue10 мая 1997 года.

* * *

ДИАЛОГ ИЗ ФИЛЬМА «Я, РОБОТ»