Хавьер Фресан - Том. 22. Сон разума. Математическая логика и ее парадоксы

Рассмотрим пример. Вместо того чтобы считать людей ниже 1,60 м низкими, выше 1,90 м — высокими, мы понизим границу множества и будем считать низкими людей ниже 1,50 м, далее степень принадлежности ко множеству будет постепенно возрастать, как и ранее, до значения 1,90 м. Таким образом мы получим еще одно нечеткое множество высоких людей. Степень принадлежности автора к этому множеству будет равна уже не 0,5, а 0,625. Согласно Заде, первое множество содержится во втором, и это соответствует интуитивному представлению о том, что высокие люди остаются таковыми, даже если снизить нижнюю границу множества.

Описав нечеткую логику, Лотфи Заде, изучавший электротехнику, предположил, что новую логику можно применить при обработке информации и распознавании образов — в двух областях, где нечеткость играет определяющую роль. История показала, что Заде недооценил свою идею, и наиболее широко созданная им логика применяется именно в той стране, жители которой едят чайные трюфели «со сливками, без сливок или как-то еще». В конце 90-х годов в японских магазинах начали продаваться копировальные аппараты и стиральные машины с нечеткой логикой, а в небоскребах Токио стали устанавливать лифты, нечеткая логика которых позволяла сводить время ожидания к минимуму. Как говорилось в рекламном ролике одной из этих стиральных машин, наступила нечеткая эра.

* * *

СТИРАЛЬНЫЕ МАШИНЫ С НЕЧЕТКОЙ ЛОГИКОЙ

Чтобы оптимизировать длительность и качество стирки, полезно точно указать, является одежда очень грязной, слегка грязной или практически чистой. Простейшие стиральные машины с нечеткой логикой присваивают каждой загрузке белья значение загрязнения от 0 до 1. Затем к фиксированному интервалу стирки продолжительностью в десять минут добавляется определенное время в зависимости от степени загрязнения одежды. Машина может, например, определить, что для чистого белья (0) достаточно базового времени стирки, а для очень грязного (1) — на две минуты больше. Следовательно, если мы положим в стиральную машину слегка грязную рубашку, продолжительность стирки увеличится на одну минуту. В других, более сложных моделях, с целью экономии электроэнергии учитывается степень жирности (жирные пятна отстирываются тяжелее других) и вес загруженного белья.

* * *

«Любовь» и «справедливость» — слишком расплывчатые понятия, чтобы их можно было описать двоичной логикой. Множество оттенков серого, простирающееся между «он меня любит» и «он меня не любит», между виной и невиновностью, описывается нечеткой логикой. С ростом сложности возникает потребность в новом мышлении. Следовательно, полезно ввести оценку сложности понятий, однако само понятие «сложность» не поддается попыткам дать ему определение. Даже в царстве математики, где правит абсолютная точность, нельзя однозначно отделить сложные проблемы от простых. Именно это происходит и с машинами Тьюринга: если в прошлой главе работа с идеальными компьютерами позволила нам получить теоретические результаты, касающиеся проблем, которые не может решить машина, то теперь нас интересует, какие расчеты она может провести с учетом ограничений в объеме памяти и времени выполнения программ. Именно так, за неимением лучшего определения, мы будем отличать простые задачи от сложных.

В первом приближении мы можем определить сложность как число операций, необходимых для решения задачи. Представим коммивояжера, которому нужно посетить несколько городов, после чего вернуться в исходный. Следовательно, его целью будет максимально сократить пройденный путь. Если этими городами будут, например, Париж (П), Лондон (Л), Берлин (Б) и Рим (Р) и коммивояжер начинает поездку в Париже, то его секретарь может составить расписание шестью разными способами: ПЛБРП, ПЛРБП, ПБЛРП, ПБРЛП, ПРБЛП и ПРЛБП. Учитывая примерные расстояния Париж — Лондон (455 км), Париж — Берлин (1050 км), Париж — Рим (1435 км), Лондон — Берлин (1095 км), Лондон — Рим (1855 км) и Берлин — Рим (1515 км), можно рассчитать общую длину каждого маршрута и выбрать кратчайший из них:

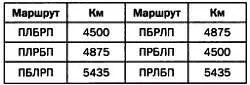
Учитывая данные, представленные в таблице, оптимальным будет маршрут Париж — Лондон — Берлин — Рим — Париж или он же, но в обратном направлении: Париж — Рим — Берлин — Лондон — Париж. Но что произойдет, если коммивояжеру нужно будет посетить не три города, а четыре, пять или любое другое количество городов? Для решения этой задачи всего для двадцати городов компьютеру средней производительности потребуется 80 тысяч лет, и в свете этого возможная потеря времени от неправильного выбора маршрута уже несущественна.