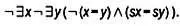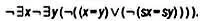
Рис. 2. Объединение двух множеств, соответствующее дизъюнкции Р V Q .

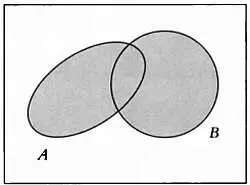
Рис. 3. Дополнение множества, соответствующее отрицанию ¬ Р .
Диаграммы Венна, на которых представлены операции пересечения (рис. 1), объединения (рис. 2) и дополнения (рис. 3) множеств.
Сделав замечание о том, как представляются выражение «для всех» и конъюнкция высказываний (логическое «и»), рассмотрим, как переводятся в формальную систему арифметики некоторые аксиомы Пеано. Первая аксиома Пеано звучит так: «Ноль есть натуральное число». Эта аксиома не требует перевода, так как мы включили символ 0 в созданный нами язык. Перейдем ко второй аксиоме: «Каждое натуральное число имеет число, следующее за ним». В этой аксиоме фигурируют две переменные: рассматриваемое натуральное число, которое мы будем обозначать через х , и следующее за ним, которое будем обозначать через у . Вспомним, что число, следующее за данным, записывается с помощью буквы s , которая ставится перед этим числом, и выражается формулой у = sx , то есть « у равно числу, следующему за х ». Следующий шаг заключается в том, что высказывание «каждое натуральное число» равносильно высказыванию «для всех натуральных чисел», и в этом контексте слово «имеет» означает «существует». Таким образом, аксиома принимает вид: «Для всякого натурального числа х существует натуральное число у такое, что у = sx ». Если бы мы могли использовать символ , то на этом можно было бы остановиться: аксиома записывалась бы как x 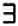 y ( y = sx ) — скобки мы использовали, чтобы выделить свойство, которым обладают числа х и у . Так как этот символ применить нельзя, нужно выполнить еще одно действие: так как «для всякого натурального числа х существует натуральное число у такое, что у = sx » равносильно «не существует натурального числа х такого, что для него не существует натурального числа у такого, что у = sx », и вторая аксиома Пеано будет записываться так: ¬ х у ( у = sx ). После столь подробных объяснений читатель может самостоятельно убедиться в том, что третья аксиома Пеано, «0 не следует ни за каким натуральным числом», соответствует выражению ¬ х ( sx = 0).
y ( y = sx ) — скобки мы использовали, чтобы выделить свойство, которым обладают числа х и у . Так как этот символ применить нельзя, нужно выполнить еще одно действие: так как «для всякого натурального числа х существует натуральное число у такое, что у = sx » равносильно «не существует натурального числа х такого, что для него не существует натурального числа у такого, что у = sx », и вторая аксиома Пеано будет записываться так: ¬ х у ( у = sx ). После столь подробных объяснений читатель может самостоятельно убедиться в том, что третья аксиома Пеано, «0 не следует ни за каким натуральным числом», соответствует выражению ¬ х ( sx = 0).
* * *
ЧЕТВЕРТАЯ АКСИОМА ПЕАНО
Переведем в формальную систему арифметики четвертую аксиому Пеано, которая гласит: «за двумя различными натуральными числами следуют различные натуральные числа». Сначала определим переменные, используемые в высказывании: это два натуральных числа, хи у. Аксиома гласит, что не могут одновременно выполняться два следующих условия: х и уразличны, следующие за ними числа совпадают. Иными словами, не существует чисел х и утаких, что:
1) хотличается от у;
2) число, следующее за х, равно числу, следующему за у.
Если бы символ конъюнкции был частью определенного нами языка, то эта аксиома записывалась бы так:
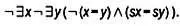
Так как использовать символ конъюнкции нельзя, нужно переписать это выражение, применяя функции отрицания и дизъюнкции. С учетом того, что отрицание отрицания высказывания равносильно исходному высказыванию, четвертая аксиома Пеано примет вид:
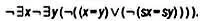
* * *
От языка — к метаязыку
Благодаря описанному выше процессу арифметика была очищена от значений и сведена к формальному каркасу. Теперь ее аксиомы являются исключительно последовательностями абстрактных символов, а доказательства превратились в упражнения по комбинаторике. Однако мы по-прежнему можем сформулировать высказывания со смыслом: например, мы можем сказать «вторая аксиома Пеано длиннее третьей», «квантор существования упоминается во второй аксиоме Пеано два раза» или «формула ¬(0 = 1) является теоремой арифметики». Важно, что здесь речь идет уже не о формализованных высказываниях языка L , а о фразах на русском языке, которые относятся к формулам L . В этих фразах говорится уже не о числах, а о высказываниях о числах, таким образом, они выходят за пределы математики в область метаматематики. Этот переход подобен ситуации, когда один из героев романа начинает писать свой роман. Подобно тому, как литература порой превращается в металитературу, математика может превратиться в метаматематику.
Читать дальше



 y ( y = sx ) — скобки мы использовали, чтобы выделить свойство, которым обладают числа х и у . Так как этот символ применить нельзя, нужно выполнить еще одно действие: так как «для всякого натурального числа х существует натуральное число у такое, что у = sx » равносильно «не существует натурального числа х такого, что для него не существует натурального числа у такого, что у = sx », и вторая аксиома Пеано будет записываться так: ¬ х у ( у = sx ). После столь подробных объяснений читатель может самостоятельно убедиться в том, что третья аксиома Пеано, «0 не следует ни за каким натуральным числом», соответствует выражению ¬ х ( sx = 0).
y ( y = sx ) — скобки мы использовали, чтобы выделить свойство, которым обладают числа х и у . Так как этот символ применить нельзя, нужно выполнить еще одно действие: так как «для всякого натурального числа х существует натуральное число у такое, что у = sx » равносильно «не существует натурального числа х такого, что для него не существует натурального числа у такого, что у = sx », и вторая аксиома Пеано будет записываться так: ¬ х у ( у = sx ). После столь подробных объяснений читатель может самостоятельно убедиться в том, что третья аксиома Пеано, «0 не следует ни за каким натуральным числом», соответствует выражению ¬ х ( sx = 0).