
* * *
В упрощенной версии формальная система арифметики, предложенная Расселом и Уайтхедом в «Началах математики», состояла из следующих основных символов: 0(число ноль), s(функция следования), ¬(отрицание), V(дизъюнкция «или»), 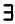 (существование), = (равенство) и открывающая и закрывающая скобки. Позднее к этим символам были добавлены переменные х, у, z типа 0, которые обозначали натуральные числа, а также переменные А, В, С типа 1, то есть множества натуральных чисел, и т. д. по мере того, как требовались элементы все новых и новых типов. Возможно, внимательный читатель заметил отсутствие других символов, которые должны быть частью языка: например, наряду с квантором существования, благодаря которому можно формализовать высказывания вида «существует натуральное число, обладающее свойством Р », можно было бы добавить еще один символ, который означал бы «для всех», как в высказывании «для всех натуральных чисел выполняется утверждение Р ». По сути, этот универсальный квантор очень широко используется в математике: «для всех» обозначается символом
(существование), = (равенство) и открывающая и закрывающая скобки. Позднее к этим символам были добавлены переменные х, у, z типа 0, которые обозначали натуральные числа, а также переменные А, В, С типа 1, то есть множества натуральных чисел, и т. д. по мере того, как требовались элементы все новых и новых типов. Возможно, внимательный читатель заметил отсутствие других символов, которые должны быть частью языка: например, наряду с квантором существования, благодаря которому можно формализовать высказывания вида «существует натуральное число, обладающее свойством Р », можно было бы добавить еще один символ, который означал бы «для всех», как в высказывании «для всех натуральных чисел выполняется утверждение Р ». По сути, этот универсальный квантор очень широко используется в математике: «для всех» обозначается символом 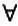 . Мы действительно можем добавить к языку символ , однако этого на самом деле не требуется, так как выражение «для всех натуральных чисел выполняется высказывание Р » равносильно выражению «не существует такого натурального числа, для которого не выполнялось бы высказывание Р ». Следовательно, символ можно выразить с помощью символов отрицания и существования.
. Мы действительно можем добавить к языку символ , однако этого на самом деле не требуется, так как выражение «для всех натуральных чисел выполняется высказывание Р » равносильно выражению «не существует такого натурального числа, для которого не выполнялось бы высказывание Р ». Следовательно, символ можно выразить с помощью символов отрицания и существования.
Это же справедливо и для конъюнкции «и»: для ее обозначения существует символ 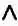 , однако он является избыточным, так как его можно заменить символами Vи ¬. Чтобы доказать это, рассмотрим три операции теории множеств: дополнение, объединение и пересечение.
, однако он является избыточным, так как его можно заменить символами Vи ¬. Чтобы доказать это, рассмотрим три операции теории множеств: дополнение, объединение и пересечение.
Для данного множества А , которое содержится в другом множестве В , дополнением множества А до В называют множество, состоящее из элементов, принадлежащих В , но не А . Например, дополнением множества гласных { а, е, i, о, и } английского алфавита является множество согласных. Рассмотрим операции объединения и пересечения. Для данных множеств X и Y их пересечение X 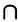 Y определяется как множество элементов, одновременно принадлежащих X и Y . Например, если X — множество четных чисел 0, 2, 4, 6, 8, 10…, а Y — множество чисел, кратных трем, 0, 3, 6, 9, 12, 15 …, то чтобы найти их пересечение, нужно определить их общие элементы: ими будут 0, 6, 12, 18…, то есть числа, кратные шести. Объединением множеств X U Y называется множество, которому принадлежат все элементы X и все элементы Y . В предыдущем примере первыми элементами объединения X и Y будут 0, 2, 3, 4, 6, 8, 9…
Y определяется как множество элементов, одновременно принадлежащих X и Y . Например, если X — множество четных чисел 0, 2, 4, 6, 8, 10…, а Y — множество чисел, кратных трем, 0, 3, 6, 9, 12, 15 …, то чтобы найти их пересечение, нужно определить их общие элементы: ими будут 0, 6, 12, 18…, то есть числа, кратные шести. Объединением множеств X U Y называется множество, которому принадлежат все элементы X и все элементы Y . В предыдущем примере первыми элементами объединения X и Y будут 0, 2, 3, 4, 6, 8, 9…
Похожесть символов, обозначающих пересечение двух множеств ( ) и конъюнкцию двух высказываний ( ), а также символов, обозначающих объединение двух множеств ( U) и дизъюнкцию двух высказываний ( V), вовсе не случайна. Если сопоставить свойствам Р и Q множества чисел, обладающих этими свойствами, например X и Y , то числа, обладающие свойствами Р и Q одновременно, будут элементами пересечения множеств X Y , а числа, обладающие свойством Р или Q , то есть как минимум одним из этих двух свойств, будут принадлежать объединению множеств X U Y . Дополнение множества, в свою очередь, соответствует отрицанию высказывания. Для представления дополнений, объединений и пересечений множеств очень удобно использовать диаграммы, созданные британским математиком и философом Джоном Венном в 1880 году. С их помощью можно доказать, что конъюнкция свойств Р и Q равносильна отрицанию дизъюнкции отрицаний Р и Q , иными словами, Р Q = ¬( ¬ Р V ¬ Q ). Это свойство позволяет выразить через Vи ¬.
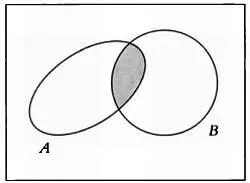
Рис. 1. Пересечение двух множеств, соответствующее конъюнкции P Q .
Читать дальше


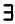 (существование), = (равенство) и открывающая и закрывающая скобки. Позднее к этим символам были добавлены переменные х, у, z типа 0, которые обозначали натуральные числа, а также переменные А, В, С типа 1, то есть множества натуральных чисел, и т. д. по мере того, как требовались элементы все новых и новых типов. Возможно, внимательный читатель заметил отсутствие других символов, которые должны быть частью языка: например, наряду с квантором существования, благодаря которому можно формализовать высказывания вида «существует натуральное число, обладающее свойством Р », можно было бы добавить еще один символ, который означал бы «для всех», как в высказывании «для всех натуральных чисел выполняется утверждение Р ». По сути, этот универсальный квантор очень широко используется в математике: «для всех» обозначается символом
(существование), = (равенство) и открывающая и закрывающая скобки. Позднее к этим символам были добавлены переменные х, у, z типа 0, которые обозначали натуральные числа, а также переменные А, В, С типа 1, то есть множества натуральных чисел, и т. д. по мере того, как требовались элементы все новых и новых типов. Возможно, внимательный читатель заметил отсутствие других символов, которые должны быть частью языка: например, наряду с квантором существования, благодаря которому можно формализовать высказывания вида «существует натуральное число, обладающее свойством Р », можно было бы добавить еще один символ, который означал бы «для всех», как в высказывании «для всех натуральных чисел выполняется утверждение Р ». По сути, этот универсальный квантор очень широко используется в математике: «для всех» обозначается символом 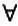 . Мы действительно можем добавить к языку символ , однако этого на самом деле не требуется, так как выражение «для всех натуральных чисел выполняется высказывание Р » равносильно выражению «не существует такого натурального числа, для которого не выполнялось бы высказывание Р ». Следовательно, символ можно выразить с помощью символов отрицания и существования.
. Мы действительно можем добавить к языку символ , однако этого на самом деле не требуется, так как выражение «для всех натуральных чисел выполняется высказывание Р » равносильно выражению «не существует такого натурального числа, для которого не выполнялось бы высказывание Р ». Следовательно, символ можно выразить с помощью символов отрицания и существования.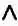 , однако он является избыточным, так как его можно заменить символами Vи ¬. Чтобы доказать это, рассмотрим три операции теории множеств: дополнение, объединение и пересечение.
, однако он является избыточным, так как его можно заменить символами Vи ¬. Чтобы доказать это, рассмотрим три операции теории множеств: дополнение, объединение и пересечение.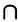 Y определяется как множество элементов, одновременно принадлежащих X и Y . Например, если X — множество четных чисел 0, 2, 4, 6, 8, 10…, а Y — множество чисел, кратных трем, 0, 3, 6, 9, 12, 15 …, то чтобы найти их пересечение, нужно определить их общие элементы: ими будут 0, 6, 12, 18…, то есть числа, кратные шести. Объединением множеств X U Y называется множество, которому принадлежат все элементы X и все элементы Y . В предыдущем примере первыми элементами объединения X и Y будут 0, 2, 3, 4, 6, 8, 9…
Y определяется как множество элементов, одновременно принадлежащих X и Y . Например, если X — множество четных чисел 0, 2, 4, 6, 8, 10…, а Y — множество чисел, кратных трем, 0, 3, 6, 9, 12, 15 …, то чтобы найти их пересечение, нужно определить их общие элементы: ими будут 0, 6, 12, 18…, то есть числа, кратные шести. Объединением множеств X U Y называется множество, которому принадлежат все элементы X и все элементы Y . В предыдущем примере первыми элементами объединения X и Y будут 0, 2, 3, 4, 6, 8, 9…











