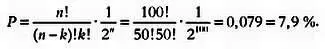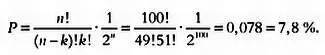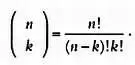
Вероятность выпадения k сторон, следовательно, равна 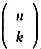 разделенному на число комбинаций орлов и решек, которое, напомним, равно 2 n . Поскольку в этом распределении вероятностей используется биномиальный коэффициент, оно известно как биномиальное распределение и может быть легко расширено на фальшивые монеты, где вероятность выпадения решки больше, чем орла, или наоборот.
разделенному на число комбинаций орлов и решек, которое, напомним, равно 2 n . Поскольку в этом распределении вероятностей используется биномиальный коэффициент, оно известно как биномиальное распределение и может быть легко расширено на фальшивые монеты, где вероятность выпадения решки больше, чем орла, или наоборот.
Биномиальное распределение позволяет сделать прогнозы, которые, как кажется, противоречат здравому смыслу. Например, какова вероятность выпадения 50 орлов за 100 бросков? Применим нашу формулу, помня, что вероятность — это отношение к единице, а не к 100:
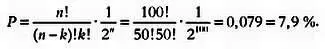
Этот результат может показаться удивительным, мы ведь ожидали 50 орлов на 100 бросков. Почему же вероятность получилась такой низкой? Ответ в том, что мы интересуемся вероятностью выпадения именно 50 орлов. Теперь найдем вероятность выпадения сорока девяти:
* * *
ПАРАДОКС МОНТИ ХОЛЛА
Парадокс Монти Холла — это применение теории вероятностей, противоречащее обычной интуиции. Представьте конкурс, когда игроку предлагается на выбор три двери, за одной из которых — ценный приз.
Конкурс состоит из двух частей: в первой части конкурсант выбирает дверь, но не открывает ее. При этом ведущий открывает одну из двух оставшихся дверей и показывает, что приза за ней нет. Во второй части конкурсант должен или сохранить свой первоначальный выбор, или изменить его на ту дверь, которую осталось открыть.
Большинство людей считают, что изменение выбора не имеет значения: вероятность того, что игрок выбрал правильную дверь, 50 %, поскольку есть две двери и приз. Однако это не так: лучшая стратегия — изменить выбор.
Объяснить это можно следующим образом: вероятность выбора правильной двери составляет одну треть. И после того, как ведущий убрал один из вариантов, вероятность того, что игрок выбрал правильную дверь, не изменилась: она по-прежнему равна одной трети. Но вероятность того, что приз за оставшейся дверью — 66 %.
Хотя люди считают эту проблему очень сложной, недавние эксперименты с голубями показали, что у этих птиц статистические способности выше, чем у нас, потому что после нескольких попыток они всегда выбирают смену двери.
* * *
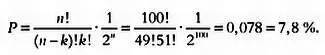
Полученное число несколько меньше, но относительно высоко. Получаем, что вероятность выпадения 48 орлов равна 7,3 %. Следовательно, вероятность выпадения числа орлов между 48 и 52 равна:
Р = Р 48 + Р 49 + Р 50 + Р 51 + Р 52 = Р 50 + 2 Р 49 + 2 Р 48 = 7,9 + 2·7,8 + 2·7,3 = 38,1 %.
Распределение вероятностей максимально для 50 орлов и уменьшается по мере того, как мы отдаляемся от центра, что и показано на графике.
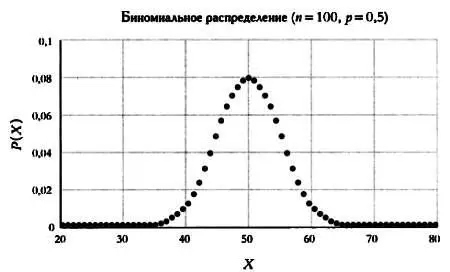
Биномиальное распределение для различного числа бросков ( n) и вероятности получения орла ( р).
Итак, хотя вероятность выпадения ровно 50 орлов невысока, мы можем быть достаточно уверены в том, что получим от 45 до 55 орлов. Этот способ рассуждения используется при проведении социальных опросов.
Предположим, что 50 % жителей страны проголосуют за определенного кандидата. Если мы проведем опрос тысячи людей, выбранных случайно, крайне маловероятно, что ровно 500 из них ответят, что проголосуют за этого кандидата. Однако гораздо более вероятно, что таким будет ответ от 450 до 550 опрошенных. Способ увериться в том, что опрос достоверный, — установить, между какими двумя величинами заключено 95 % вероятности получить необходимый результат.
Биномиальное распределение — это только одно из многочисленных дискретных распределений вероятностей. Кроме него, существует распределение вероятностей для непрерывных переменных, при котором нас интересует вероятность того, что какое-то значение находится в определенном диапазоне.
Самое известное непрерывное распределение вероятности — это распределение Гаусса, или нормальное распределение. Оно имеет форму колокола, как можно заметить на графике на стр. 74.
Читать дальше

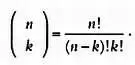
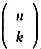 разделенному на число комбинаций орлов и решек, которое, напомним, равно 2 n . Поскольку в этом распределении вероятностей используется биномиальный коэффициент, оно известно как биномиальное распределение и может быть легко расширено на фальшивые монеты, где вероятность выпадения решки больше, чем орла, или наоборот.
разделенному на число комбинаций орлов и решек, которое, напомним, равно 2 n . Поскольку в этом распределении вероятностей используется биномиальный коэффициент, оно известно как биномиальное распределение и может быть легко расширено на фальшивые монеты, где вероятность выпадения решки больше, чем орла, или наоборот.