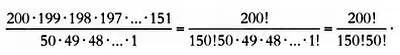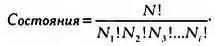Эдуардо Арройо - Том 42. Путешествие от частицы до Вселенной. Математика газовой динамики

Теперь обратим внимание на газ, обладающий некоторым количеством возможных макросостояний, каждому из которых соответствуют некоторое давление, температура и объем. Мы хотим узнать, в каком из этих макросостояний находится газ. Поскольку макроскопические характеристики газа связаны с распределением скоростей его молекул, на самом деле мы хотим узнать это распределение.

Как мы видели, для этого мы не можем воспользоваться уравнениями Гамильтона, но зато мы можем использовать различные результаты, полученные ранее: например, то, что, перейдя в состояние равновесия, газ не выйдет из него и что все микроскопические конфигурации — или микросостояния — в нашей области фазового пространства равновероятны.

Поскольку все микросостояния равновероятны, разумно предположить, что макросостояние с наибольшим числом совместимых микросостояний будет наиболее вероятным. Если вероятность некоторого макросостояния намного выше, чем у любого другого, мы можем сделать вывод, что газ находится в нем. То есть наше макросостояние будет тем, для которого распределение скоростей наиболее вероятно.

Теперь нам осталось только выяснить, какое из возможных распределений скоростей имеет самую высокую вероятность.

Чтобы рассмотреть возможные состояния, нам нужно сделать небольшое упрощение: предположим, что все молекулы могут обладать только определенными значениями энергии, а не любыми в некотором диапазоне. Как только мы получим интересующее нас выражение, мы ослабим это условие. Энергии и скорости пропорциональны, так что, узнав распределение энергии, мы получим распределение скоростей.

Присвоим число каждому из этих значений энергии, от одного до k . У нас всего N частиц; число частиц с энергией i будет обозначаться N i . То есть если у нас есть 50 частиц первого уровня энергии, то N 1 = 50. Теперь предположим, что у нас есть некоторое распределение энергии.

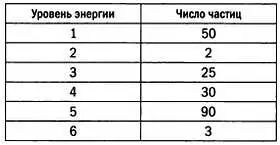
Мы хотим узнать, сколько комбинаций частиц дает нам именно это распределение. У нас всего 200 частиц, из которых 50 находятся на первом уровне энергии.

Пронумеруем наши частицы от одного до 200. Сколько существует возможных комбинаций, при которых на этом уровне находятся 20 частиц? Чтобы выяснить это, воспользуемся стратегией, очень похожей на ту, что мы применяли с биномиальным распределением.

Для первой частицы у нас есть 200 возможностей — столько, сколько у нас частиц. Для второй — 199, поскольку первая уже выбрана; для третьей — 198, и так далее. В итоге у нас получится:

200·199·198·197·…·151 возможностей.

Нам нужно разделить общее число возможных комбинаций между 50 частицами, которыми мы располагаем, так же как мы это делали с выпадением орла или решки. Так как у нас 50 частиц, получаем 50·49·…·1 возможностей. Число возможностей равно:

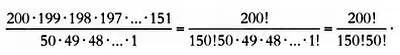
Если мы повторим эту операцию для каждого значения энергии, то получим число конфигураций, совместимых с нашим распределением. Больцман доказал, что это число можно вычислить, пользуясь факториальными функциями:

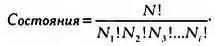
С этим уравнением очень сложно работать, так как оно содержит факториальные функции, которые, при больших значениях N , дают в результате огромные числа. Однако мы можем примерно понять возможные прогнозы.

У нашего газа есть заданная энергия. Так как она ограничена с внешней стороны, суммарная энергия не может измениться. Если бы у нас было много частиц с очень большой энергией, нам пришлось бы выбрать много частиц с небольшой энергией, чтобы компенсировать это. Поскольку количество энергии ограничено, число частиц с большой энергией также ограничено. Мы можем сделать вывод, что существует мало комбинаций, при которых у большого количества частиц очень большая энергия. Точно так же, если бы у большого количества частиц была очень небольшая энергия, нам пришлось бы выбрать много частиц с большой энергией, чтобы компенсировать это. Это означает, что сокращается число вариантов и, следовательно, существует мало комбинаций со значительным числом частиц с очень большой или очень небольшой энергией.

* * *

ВЫВЕДЕНИЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ БОЛЬЦМАНА