Эдуардо Арройо - Том 42. Путешествие от частицы до Вселенной. Математика газовой динамики

* * *

ДРУГИЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

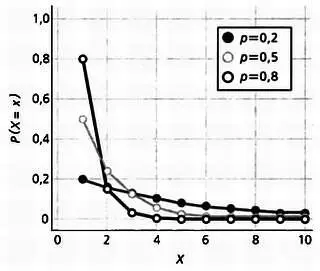
Другое широко используемое распределение — это геометрическое распределение. Как и в случае с биномиальным распределением, у нас есть случайное событие, такое как бросок кубика или монеты. Назовем успехом один из возможных вариантов, например выпадение орла. Какова вероятность того, что первый успех появится после к бросков, если его вероятность равна р?

Геометрическое распределение говорит, что эта вероятность вычисляется по

Р = (1 — р) k-1 р,

что можно представить следующим образом.

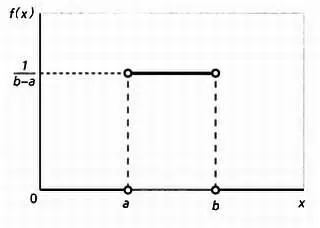
Среди распределений вероятности, где переменная может принимать любое значение в определенном диапазоне, самое простое — равномерное распределение, при котором каждому событию просто назначается одна и та же вероятность, так что получается фигура, подобная этой.

* * *

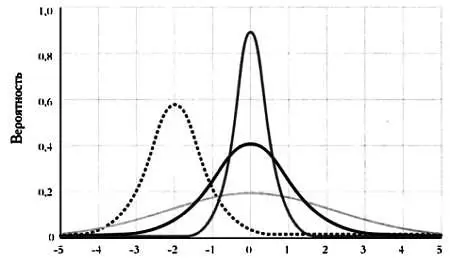
Различные формы нормального распределения, согласно разным параметрам.

Нормальное распределение имеет большое значение как в статистике, так и в естественных и социальных науках, благодаря центральной предельной теореме. В ней говорится, что в некоторых условиях любая случайная переменная имеет тенденцию следовать нормальному распределению. Например, если мы будем измерять такую физическую величину, как скорость, наши результаты будут иметь тенденцию распределяться согласно фигуре, изображенной на графике, вокруг среднего значения. Именно использование этого распределения позволяет физикам определить границы доверия своим экспериментам: измерив площадь под кривой Гаусса, можно получить вероятность того, что результат измерения случаен.

Нормальное распределение можно наблюдать практически во всех областях знания, и оно имеет очень широкое практическое применение. Например, результаты любого экзамена имеют тенденцию следовать нормальному распределению вокруг средней оценки. Этот фактор можно использовать при вычислении нормализованных оценок, то есть оценка каждого студента определяется в зависимости от положения на кривой. Распределение скоростей молекул газа также следует этому распределению, как будет показано далее.

Нормальное распределение связано с биномиальным распределением, о котором мы говорили ранее. При очень большом числе попыток биномиальное распределение описывает кривую Гаусса.

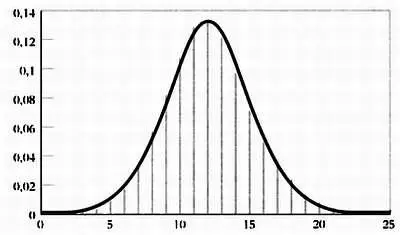
Связь между биномиальным и нормальным распределениями. Прямые показывают биномиальное распределение, вокруг которого проходит нормальное распределение.

Действительно, для получения знаменитого распределения вероятностей для газа Больцман начал рассматривать дискретные значения энергии как биномиальную функцию и затем перешел к бесконечно большому их числу, что привело его к распределению Гаусса.

Познакомившись с теорией вероятностей, пора применить полученные знания к описанию газа. Для этого нам потребуются такие понятия, как микросостояния и макросостояния.

Предположим, что у нас есть газ, обладающий некоторым давлением, объемом и температурой. Нам известны макроскопические характеристики газа, но мы не знаем, под каким давлением находится каждая его молекула и с какой скоростью она движется. Итак, можно сказать, что мы знаем макроскопическое состояние газа, но не микроскопическое. Это макроскопическое состояние газа называется макросостоянием.

Макросостоянию могут соответствовать тысячи миллионов микроскопических состояний: например, поменяв положение и скорость любой пары частиц, мы получаем систему, на первый взгляд, с теми же свойствами. Поскольку у нас тысячи миллионов частиц, существует огромное количество микроскопических состояний, согласующихся с тем, что мы наблюдаем в лаборатории. Эти микроскопические состояния, которых невозможно добиться экспериментально, называются микросостояниями. Каждому макросостоянию в целом соответствуют тысячи миллионов микросостояний, которые порождают одно и то же поведение в крупном масштабе.