Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

Вспомним формулу (*) из прошлого раздела:

3 C 3 + 2 C 4 + C 5 = 12 + 2 V 4 + 4 V 5 + … + С 7 + 2 С 8 + … (*)

Заметим, что выражение в правой части больше или равно 12, то есть всегда выполняется соотношение

3 С 3 + 2 С 4 + С 5 >= 12.

Кроме того, С 3, С 4 и С 5 не могут быть равны нулю одновременно. Можно сформулировать следующую теорему:

« В любом выпуклом многограннике всегда существует как минимум одна грань в форме треугольника, четырехугольника или пятиугольника ».

Другие грани могут иметь любую форму, но как минимум одна грань должна иметь три, четыре или пять ребер. Вспомним, что правильным многогранником называется выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и во всех вершинах которого сходится одинаковое число ребер. Тогда предыдущую теорему можно записать так:

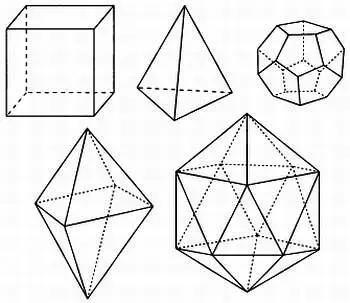
« Единственными правильными многогранниками являются тетраэдр, октаэдр, икосаэдр, куб и додекаэдр ».

* * *

ГРАФЫ, СООТВЕТСТВУЮЩИЕ ПРАВИЛЬНЫМ МНОГОГРАННИКАМ

Пять правильных многогранников необязательно изображать в перспективе — можно построить соответствующие им плоские графы. Значения V, Аи Сдля следующих фигур представлены в таблице ниже.

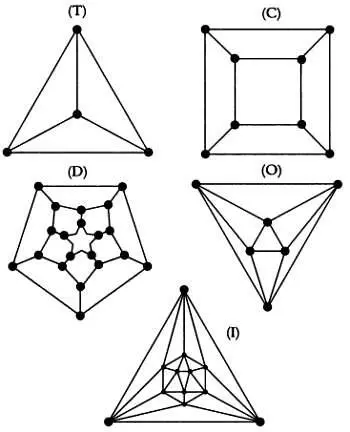
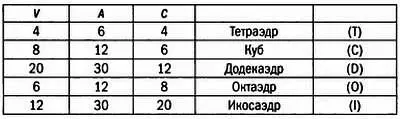
Заметим, что в полученной нами теореме общее соотношение Эйлера сочетается с характеристиками многоугольников, ограничивающих часть пространства, образующего многогранник.

* * *

Исходя из полученного результата (всегда будет существовать грань в форме треугольника, четырехугольника или пятиугольника) и из определения правильного многогранника получим, что единственно возможные правильные многогранники будут полностью образованы либо равносторонними треугольниками, либо квадратами, либо правильными пятиугольниками.

Если все грани многогранника — равносторонние треугольники (их углы равны 60°), формула (*) сводится к 3 С 3 = 12 + 2 V 4 + 4 V 5. В тетраэдре С 3 = 4 (и, разумеется, V 3 = 4, V 4 = V 5 = 0). Для октаэдра V 4 = 6, V 3 = V 5 = 0 и С 3 = 8. В икосаэдре С 3 = 20 и V 5 = 12.

Если все грани многогранника — квадраты, то в его вершинах могут сходиться только три ребра, поэтому V 4 = V 5 = 0 и по формуле (*) 2 С 4 = 12, то есть С 4 = 6. Таким образом, этот многогранник — куб.

Если все грани многогранника — правильные пятиугольники, то степень его вершин может равняться только 3. По формуле (*) С 5 = 12 — это додекаэдр.

* * *

ТОЧНЫЙ ПОДСЧЕТ

Пусть Р— выпуклый многогранник с r( Р ) гранями. Рассмотрим два его параметра:

r( Р ) — количество натуральных чисел i, таких что в Рсуществует грань с iребрами;

К( Р ) — число сторон грани Р с наибольшим числом вершин или ребер.

Так, в кубе Р r( Р ) = 1, К( Р ) = 4. Для пирамиды Р, в основании которой лежит пятиугольник, r( Р ) = 2, К( Р ) = 5.

Если многоугольник Римеет грань, число сторон которой равно К( Р ), так как каждая из этих сторон является ребром другой грани, то общее число граней будет равно как минимум К( Р ) + 1, то есть

С( Р ) >= К( Р ) + 1.

Так как r( Р ) не может быть больше, чем число элементов множества {3, 4, 5, К( Р )}, то

r( Р ) = < К( Р ) — 2.

На основании вышеприведенных неравенств для С( Р ) и r( Р ) имеем:

С( Р ) — r( Р ) >= К( Р ) + 1 — ( К(Р) — 2) = 3.

Если бы все грани многогранника были бы различны, то выполнялось бы равенство С( Р ) = r( Р ) + 3, что невозможно.

* * *

Если вы не привыкли следовать правилам, то возможно, что вы задавались вопросом, существуют ли фигуры без повторяющихся элементов. Например, существует ли многогранник, все стороны которого являются различными многоугольниками: один треугольник, один четырехугольник, один пятиугольник и так далее. Это был бы образцовый многогранник — он мог бы поворачиваться разными сторонами и демонстрировать разные многоугольники. Живительно, но подобный многоугольник не может существовать. И этому есть очень красивое доказательство, в котором используются методы комбинаторики.