Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

* * *

ФОРМУЛА НА МАРКАХ

На этой марке, выпущенной в ГДР в честь Леонарда Эйлера, изображен икосаэдр и формула A— C+ V = 2 в немецком варианте. Интересный способ рассказать о формуле всему свету.

* * *

Помимо формулы Эйлера и ее удивительных следствий, существует множество других областей геометрии, где теория графов представляет особый интерес. Далее мы приведем несколько примеров.

Гамильтоновы циклы в многогранниках

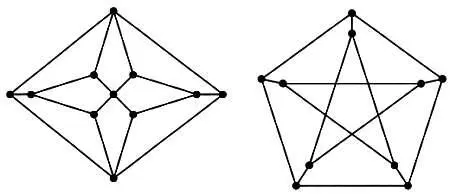
Мы уже рассказали о том, что Гамильтон впервые представил цепи, которые сегодня носят его имя, в игре, где нужно было обойти по разу все вершины додекаэдра. (Напомним, гамильтоновы цепи — это пути в графе, которые проходят через все его вершины ровно по одному разу.) Именно поэтому позднее были предприняты попытки найти гамильтоновы цепи во всех возможных многогранниках либо показать, что они не существуют. На следующих рисунках представлены так называемый граф Гершеля и граф Петерсена — два примера графов, в которых не существует гамильтоновых цепей. Попробуйте убедиться в этом самостоятельно, проведя карандашом линию, проходящую через все вершины этих графов ровно один раз.

Перейдем в трехмерное пространство. Следуя по пути Гарольда Коксетера, попробуем отыскать гамильтоновы цепи в других многогранниках. Коксетер весьма хитроумным способом решил эту задачу для ромбододекаэдра.

Все грани ромбододекаэдра равны, но в его вершинах сходится разное число ребер, поэтому он не является правильным многогранником.

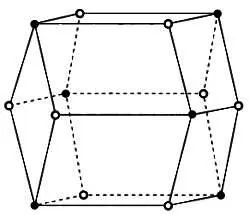
Этот любопытный многогранник, представленный на рисунке, в соответствии с названием, имеет 12 равных граней, которые являются параллелограммами, и обладает интересным свойством: в восьми его вершинах сходится по три ребра (такие вершины обозначены кругами белого цвета), в оставшихся шести вершинах сходится по четыре ребра (такие вершины обозначены кругами черного цвета). Заметьте, что вершины, выделенные белым цветом, являются вершинами воображаемого куба. Следовательно, ромбододекаэдр можно считать кубом, дополненным шестью пирамидами, в основаниях которых находятся квадраты. Его объем равен удвоенному объему вписанного куба. Ромбододекаэдрами, так же как и кубами, можно заполнить пространство — получится мозаика в трехмерном пространстве.

Существует ли гамильтонова цепь в ромбододекаэдре? Коксетер отвечает на этот вопрос решительным «нет», приводя гениальное доказательство: если бы в ромбододекаэдре существовала гамильтонова цепь, которая бы начиналась и заканчивалась в одной из его вершин, то она проходила бы через 14 вершин по одному разу, причем каждый раз цвет вершин чередовался (с черного на белый или с белого на черный). Такое чередование цветов невозможно, так как в черный цвет окрашено шесть вершин, а в белый — восемь.

* * *

ГАРОЛЬД КОКСЕТЕР (1907–2003)

Гарольд Скотт Макдональд Коксетер родился в Лондоне, изучал математику в Тринити-колледже Кембриджа, но вся его научная карьера прошла в Канаде, в Торонтском университете, где он проработал 60 лет. Его считают одним из величайших геометров XX века, он является автором 12 важных трудов и множества работ, выполненных в соавторстве с другими блестящими геометрами. Он внес неизмеримый вклад в изучение многогранников, в частности многогранников, расположенных в пространстве, имеющем более трех измерений. Коксетер дружил со знаменитым голландским художником М. Эшером, который отразил в своих картинах множество свойств, открытых Коксетером.

* * *

Графы на неплоских поверхностях

Хотя графы обычно изображаются на плоскости, задачи о раскраске графов и анализ их планарности стимулировали изучение графов, расположенных на других поверхностях: сферах, торах, цилиндрах и так далее. Графы также изображаются в трехмерном пространстве, как, например, при решении задач теории узлов.

Анализ графов на различных поверхностях помог определить множество топологических свойств, которые являются инвариантными относительно непрерывных деформаций и лежат в основе классификации кривых и поверхностей. Представим надутый шарик, на поверхности которого фломастером нарисован граф. Если мы будем сминать шарик (но так, чтобы он не лопнул), то заметим, что свойства графа будут оставаться неизменными (число вершин, ребер; число ребер, инцидентных каждой вершине, и другие свойства).