Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

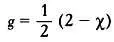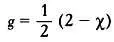
называется число отверстий в ней. Для сферы g = 0, следовательно, в тороидальных многогранниках g = 1. Итак, и g являются характеристиками поверхности, то есть число 2 в формуле С + V = А + 2 указывает на сферическую природу выпуклых многогранников. Для невыпуклых многогранников формула Эйлера не выполняется. В следующих разделах, где рассматриваются только выпуклые многогранники, мы подробно расскажем о следствиях формулы С + V = А + 2.

Теперь мы знаем ограничения на число граней С и число вершин V выпуклого многогранника. Число ребер А полностью зависит от С и V. Попробуем исключить А из формулы Эйлера.

Чтобы полностью исключить А , нужно «более явно» выразить формулу Эйлера через С и V , уточнив, что скрывается за этими числами.

В выпуклом многограннике Р с числом граней С и числом вершин V обозначим за С n число граней, имеющих n ребер, V n — число вершин, в которых сходятся n ребер. Можно записать следующую сумму ряда (конечного!):

С = С 3 + С 4 + С 5 + С 6 + … (1)

Также

V = V 3 + V 4 + V 5 + V 6 + … (2)

Так как одно ребро принадлежит двум граням одновременно, то

3 С 3 + 4 С 4 + 5 С 5 + 6 С 6 + … = 2A . (3)

Так как каждое ребро соединяет две вершины, получим

3 V 3 + 4 V 4 + 5 V 3 + 6 V 6 + … = 2 A . (4)

Используя формулу Эйлера, где обе части умножены на 2, то есть 2 С + 2 V = 4 + 2 A , учитывая (1), (2) и (3), получим:

2 С 3 + 2 С 4 + 2 С 5 + 2 С 6 + … + 2 V 3 + 2 V 4 + 2 V 5 + 2 V 6 + … = 4 + 3 С 3 + 4 C 4 + 5 C 5 + 6 C 6 + …

Иными словами,

2 V 3 + 2 V 4 + 2 V 5 + 2 V 6 + … = 4 + C 3 + 2 C 4 + 3C 5+ 4 C 6 + … (5)

Аналогично на основе (1), (2) и (4) получим:

2 С 3 + 2 С 4 + 2 С 5 + 2 С 6 + … + 2 V 3 + 2 V 4 + 2 V 5 + 2 V 6 + … = 4 + 3 V 3 + 4 V 4 + 5 V 5 + 6 V 6 + …

Иными словами,

2 C 3 + 2 C 4 + 2 C 5 + 2 C 6 + … = 4 + V 3 + 2 V 4 + 3 V 5 + 4 V 6 + … (6)

Вид столь громоздких равенств разочаровывает, но мы перешли от формулы Эйлера к соотношению, которое связывает вершины и грани, и при этом в нем не учитывается число ребер.

Если прибавить к (5) выражение (6), умножив обе его части на 2, получим:

2 V 3 + 2 V 4 + 2 V 5 + 2 V 6 + … + 4 С 3 + 4 С 4 + 4 С 5 + 4 С 6 + … = 12 + С 3 + 2 С 4 + 3 С 5 + 4 С 6 +… + 2 V 3 + 4 V 4 + 6 V 5 + 8 V 6 + …

Упростив это выражение, получим удивительный результат:

3 C 3 + 2 C 4 + C 5 = 12 + 2 V 4 + 4 V 5 + … + C 7 + 2 С 8 + … (*)

В этом выражении не фигурирует число ребер, а также отсутствуют шестиугольные грани и вершины, в которых сходятся три ребра. Запомните выражение (*): оно поможет нам совершить много удивительных открытий. Например, вспомним, какую форму имеет футбольный мяч. Это многогранник, в котором сочетаются пятиугольные и шестиугольные грани, а в каждой вершине сходятся три ребра.

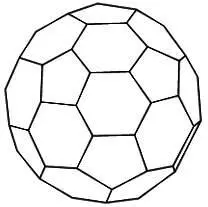
Существуют ли другие многогранники, где вершины и грани обладают теми же особенностями? Заметим, что С 3 = С 4 = С n = 0 при n >= 7, V 4 = V n = 0 при n >= 5, следовательно, согласно (*) должно выполняться равенство С 5 = 12, но С 6остается неопределенным. Б. Грюнбаум и Т. С. Моцкин доказали, что С 6 может принимать любое значение, отличное от 1. Любопытно, что пятиугольных граней именно 12.

В многограннике, образованном четырехугольниками и шестиугольниками, согласно (*) 2 С 4 = 12 + 2 V 4 + 4 V 5 + …, то есть минимум шесть его граней будут четырехугольниками. Если вершины будут иметь степень 3, то таких граней будет ровно 6. Если гранями многогранника являются треугольники и шестиугольники, то 3 С 3 = 12 + 2 V 4 + 4 V 5 + … и как минимум четыре грани будут иметь форму треугольника. Если вершины будут иметь степень 3, то треугольных граней будет ровно четыре.

Попробуйте представить себе выпуклый многогранник, у которого нет ни одной грани в форме треугольника, четырехугольника или пятиугольника. Очевидно, что такого выпуклого многогранника не существует.