Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

б) событие считается произошедшим только тогда, когда выполнены все предшествующие ему действия;

* * *

ПРИМЕР ИСПОЛЬЗОВАНИЯ СИСТЕМЫ PERT В СТРОИТЕЛЬСТВЕ

Далее приведен пример анализа строительства дома (точнее, начальных действий) по системе PERT. Нужно составить список начальных задач, присвоить каждой задаче букву или номер, а также определить зависимости и примерное время выполнения ( Т e) каждой задачи.

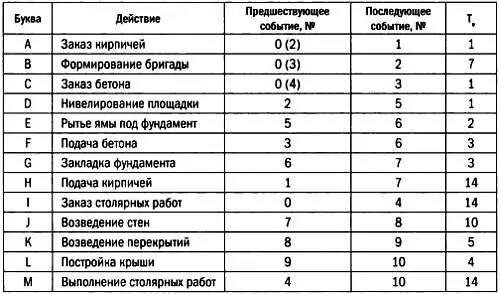
Теперь можно построить соответствующий граф, расположив рядом с каждой его вершиной квадрат и треугольник. В квадратах будем указывать день от начала работ, когда может начаться событие, в треугольниках — день его завершения.

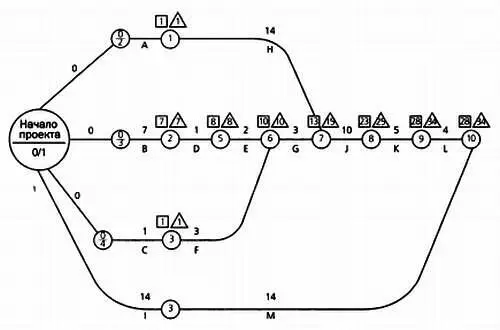
Продолжение графа (вплоть до завершения работ) приведено на следующем рисунке.

* * *

в) следует избегать ситуаций, когда предшествующее и последующее событие для двух действий совпадают. Этого можно избежать путем ввода фиктивных событий нулевой длительности;

г) необходимо создать промежуточные события и фиктивные действия, чтобы устранить вершины 4-й степени и выше;

д) никакое событие не может быть одновременно начальным и конечным в последовательности событий.

6. Наконец, анализируется построенный граф. Например, интерес представляют следующие параметры:

а) дата, наиболее удаленная от завершения проекта, то есть дата начала первого события в последовательности событий;

б) допустимый крайний срок. Завершение события позднее этого срока негативно повлияет на проект в целом;

в) продолжительность события — разница между двумя предыдущими параметрами;

г) избыток времени, доступный при реализации данного действия;

д) критический путь — путь на графе с наибольшим временем выполнения (между двумя данными событиями или для всего графа).

Так называемая система PERT/COST имеет ту же структуру, но в ней учитываются не сроки выполнения задач, а их стоимость. Система PERT также допускает комбинирование сроков и финансовых затрат. В настоящее время для всех систем планирования разработаны простые в использовании информационные системы.

Многие свойства фигур, которые изучаются в геометрии, зависят от их параметров: величин углов, расстояний, перпендикулярности прямых, площади фигур, объема тел и так далее. Однако теория графов и топология помогли выявить геометрические закономерности, которые не зависят ни от параметров геометрических фигур, ни от их формы. В этой короткой главе мы расскажем об известной формуле Эйлера и обнаружим множество ее удивительных следствий, которые проявляются в многогранниках и мозаиках.

В формуле Декарта 1640 года и формуле Эйлера 1752 года фигурируют только грани, ребра и вершины, поэтому эти формулы применимы к множеству различных фигур и по-прежнему выполняются даже после определенных преобразований.

Эти формулы дали начало новому разделу математики — топологии, которая бурно развивалась в XIX веке. Август Фердинанд Мёбиус, Бернхард Риман, Анри Пуанкаре, Ян Брауэр, Соломон Лефшец и многие другие математики, которые работали в различных областях, нашли в этой «новой геометрии» фундаментальную основу для изучения кривых, поверхностей, пространств, функций. Топология помогла определить свойства, которые нельзя было формализовать в рамках традиционной геометрии.

Август Фердинанд Мёбиус— один из математиков XIX века, интересовавшихся топологией.

Если говорить кратко, то топология свободна от жестких структур евклидовой и проективной геометрии. С помощью «непрерывных преобразований» стало возможным моделировать новые фигуры и определять новые категории преобразований. Представим себе треугольник, нарисованный на поверхности шара. При сжатии шара (таком, что шар не ломается) треугольник будет принимать различную форму. Будут изменяться углы и длины сторон, но «сущность» треугольника будет оставаться неизменной: это по-прежнему будет фигура, определяемая тремя точками и тремя отрезками, соединяющими эти точки. Чтобы начать мыслить с топологической точки зрения, нужно представить, что все фигуры сделаны из резины и могут деформироваться. Так, деформацией сферы невозможно получить бублик, но зато бублик будет эквивалентен… чайной чашке.