Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

* * *

АЛГОРИТМ КРУСКАЛА

Джозеф Бернард Крускал(1928–2010) , выпускник Принстонского университета и специалист по комбинаторике из компании Bell Laboratories, в 1950-е годы разработал замечательный алгоритм. Этот алгоритм позволяет получить минимальное остовное дерево (то есть соответствующее наименьшим общим затратам) путем последовательного добавления к нему ребер графа, упорядоченных по возрастанию веса.

* * *

Во множестве реальных ситуаций используются не обыкновенные графы, а орграфы, то есть ориентированные графы. В этих графах к ребрам добавляются стрелки, указывающие направление. Орграф, изображенный на первом рисунке снизу, может соответствовать, например, маршруту по улицам с односторонним движением. На втором рисунке снизу тот же орграф может представлять последовательность задач ( А, В, С, D, Е ) и порядок, в котором нужно выполнить эти задачи.

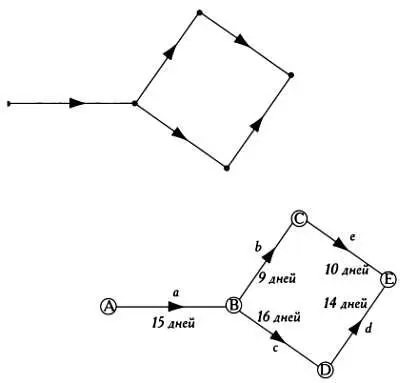
В виде орграфов можно представить энергосети, транспортные потоки, телефонные сети, схемы промышленного производства, порядок действий при ремонте и многое другое. Как можно увидеть из второго рисунка, узлы А, В, С, D, Е обозначены не точками, а кругами или прямоугольниками, внутри которых указаны задачи (разгрузка, покраска, установка и прочее), а также соответствующие им веса (1000 евро, 12 минут и так далее). На ребрах ориентированного графа, которые называются дугами, также указаны веса — это оценки затрат финансов, времени и других ресурсов, которые требуются для выполнения соответствующего действия.

Именно в таких сложных случаях требуется найти критические пути, оптимальные с точки зрения затрат или сроков. На предыдущем рисунке сумма а, Ь, е равна 34 дням, сумма а, с, d — 45 дням. Критическим путем является ABDE . Если критический путь не пройден до конца, хотя другие операции выполнены, проект не может считаться полностью завершенным.

* * *

ОПТИМИЗАЦИЯ ВРЕМЕНИ ПРЕБЫВАНИЯ САМОЛЕТОВ В АЭРОПОРТУ

Авиакомпании стремятся сократить время между приземлением и следующим взлетом самолета. После остановки самолета выполняются следующие действия:

А.Высадка пассажиров.

В.Выгрузка багажа.

С.Уборка салона.

D.Загрузка еды и напитков.

Е.Осмотр самолета.

F.Заправка горючим.

G.Загрузка нового багажа.

Н.Посадка новых пассажиров.

Некоторые из этих действий могут выполняться параллельно (например, Аи В, С и D, Еи F), другие — последовательно. К примеру, Снельзя начать, пока не закончится A, Gможно выполнить только после В и так далее. Завершающим действием является Н. К этому моменту действие Fуже выполнено, действие Gеще не закончено. Если на выполнение всех этих действий отводится 20 минут, соответствующий орграф должен быть очень точным. Критический путь этого графа непосредственно повлияет на расписание перелетов, а также на задержки рейсов и время ожидания самолета.

* * *

С начала Второй мировой войны начал формироваться широкий спектр методов оптимизации планирования. После того как СССР запустил в космос первый спутник, в США началась работа над различными крупными проектами, начиная от баллистической ракеты «Поларис», размещаемой на подводных лодках, и заканчивая высадкой человека на Луну. Для столь больших проектов требовались соответствующие методы планирования. В этих методах используются так называемые сетевые диаграммы.

К важнейшим подобным методам относятся следующие.

1. PERT( Program Evaluation and Review Technique — техника оценки и анализа программ). Была разработана по заказу ВМС США в 1958 году. Этот метод доказал свою эффективность при планировании длительных, сложных и затратных проектов.

2. СРМ(метод критического пути). Этот метод особенно подходит для планирования последовательности задач и изучения критических путей, то есть последовательности координируемых действий, невыполнение которых может вызвать задержки проекта. Похожими методами являются СРА (анализ критического пути), РЕР (процедура оценки программы), LESS (оценка наименьших затрат и планирование) и SCANS (планирование и контроль посредством автоматизированной сети).