Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

Старинный город Кёнигсбергна гравюре XVII вена.

На рисунке представлен упрощенный план города, на котором мосты обозначены цифрами, а районы города — буквами.

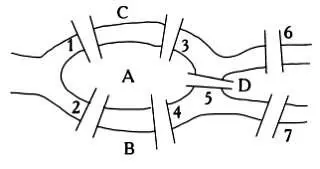
Эйлер писал об этой задаче: «Насколько я понимаю, эта задача широко известна. Она формулируется так: в прусском городе Кёнигсберге есть остров под названием Кнайпхоф, окруженный двумя рукавами реки Преголя. Через два рукава реки перекинуто семь мостов. Нужно определить, можно ли обойти все мосты, пройдя по каждому ровно один раз. Мне сообщили, что некоторые утверждают, будто это невозможно, другие сомневаются, но никто не верит, что это и в самом деле возможно».

Сам Эйлер определил, что решить задачу невозможно, приведя следующие рассуждения. Расположение районов города можно представить на схеме, где четырем точкам А, В, С и D соответствуют четыре района города, а кривым, соединяющим эти точки, — мосты:

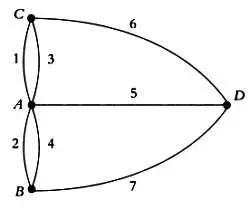
Таким образом, исходная задача эквивалентна следующей, проиллюстрированной рисунком выше: можно ли провести маршрут так, что каждая кривая будет пройдена ровно один раз? Если бы это было возможно, то число линий для каждой точки должно было быть четным (об этом рассказывается в главе 3). Однако число линий для каждой точки на схеме является нечетным. Следовательно, задача не имеет решения.

Кёнигсбергские мосты были разрушены во время Второй мировой войны, но эта история, авторство которой приписывается Эйлеру, дала начало удивительно полезной и красивой математической теории — теории графов. Нужно учитывать, что еще до ее создания многие ученые совершенно независимо друг от друга использовали понятия, которые впоследствии были объединены в теорию графов.

В 1847 году Густав Кирхгоф использовал схемы, подобные графам, при изучении электрических цепей. В 1857 году Артур Кэли изучал число изомеров органического соединения с помощью графов, в которых точки соединялись между собой одной или четырьмя линиями — по числу химических связей. В 1869 году Мари Энмон Камиль Жордан занимался анализом абстрактных древовидных структур. В 1859 году ирландский математик Уильям Роуэн Гамильтон придумал игру (о ней мы расскажем несколько позже), цель которой — обойти вершины многогранника. Несколько лет спустя на основе этой игры были созданы гамильтоновы цепи, которые имеют очень интересное применение. В 1852 году возникла задача о раскраске карт таким образом, чтобы страны с общей границей были окрашены в разные цвета. Эта задача дала начало множеству исследований графов. Психолог Курт Левин ввел в психологию схемы, на которых люди обозначались точками, а личные отношения между ними — линиями. Физики Уленбек, Ли и Янг использовали схемы из точек и линий для изображения структур молекул и взаимодействия между ними.

* * *

ЛЕОНАРД ЭЙЛЕР (1707–1783)

Эйлер был одним из величайших математиков всех времен. Он родился в Швейцарии, большую часть жизни проработал в Берлинской и Петербургской академиях наук. Он опубликовал свыше 500 трудов, а его полное собрание сочинений насчитывает 87 томов. Особо выделяются его работы по алгебре, теории чисел, геометрии, математическому анализу, механике, астрономии и физике. Его именем названо множество теорем; формул и понятий. Любопытно, что больше половины всех своих трудов он создал после того как ослеп в 1766 году. Так как именно Эйлер нашел решение задачи о кёнигсбергских мостах, его считают пионером теории графов.

* * *

Во всех этих случаях конкретная задача изображалась в виде графической схемы, или графа, состоящего из точек и соединяющих их линий. Соответственно, в ходе решения задачи использовался анализ графа. Так как одинаковые графические схемы могут описывать совершенно различные задачи, изучение этих схем позволит найти решение для множества задач одновременно. Разумеется, при построении графа всегда остаются неучтенными какие-то условия и параметры, так как граф должен быть простым. Заметим также, что построение графа не относится к задачам метрической геометрии, то есть точки графа могут соединяться линиями произвольной формы. Главное — отобразить отношения, связи и взаимодействия, а не построить фотографически точную сеть линий и точек.