Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

* * *

Дерево — это очень простой граф, все вершины которого соединены так, что отсутствуют циклы, как, например, на следующем рисунке:

В дереве можно проложить маршрут между любыми двумя вершинами.

Далее приведены все возможные деревья с числом вершин от 1 до 8.

Последовательность чисел, обозначающих количество всех возможных деревьев для каждого числа вершин, выглядит так: 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, 551, 1301, 3159…

Если дерево имеет р вершин, то в нем всегда будет р — 1 ребер, но для каждого значения р можно изобразить р р -2разных деревьев (формула Кэли). Понятие дерева впервые ввел Кэли в 1857 году. Деревья образуют очень важный класс графов, так как в них все вершины соединены минимально возможным числом ребер. Благодаря этому деревья находят интересное применение в самых разных областях: при проектировании электрических цепей, телефонных сетей, при поиске маршрутов между населенными пунктами и так далее.

Следующая простая и красивая теорема дает характеристику деревьям, а также имеет крайне важное практическое значение:

«Граф G является деревом тогда и только тогда, когда между любыми двумя различными его вершинами u и v существует единственный путь. Это равносильно следующему утверждению: С является связным графом, если он имеет р вершин и р — 1 ребро».

Несмотря на простоту этой теоремы, число возможных деревьев по мере увеличения р возрастает очень быстро.

Причина этому такова. Пусть G — дерево. Даны две вершины G, u и v . Так как граф G является связным, то существует по меньшей мере один путь между u и v . Если бы между этими вершинами существовало два пути, С 1 и С 2 , то в графе G образовался бы цикл, что невозможно. Разумеется, если между двумя произвольными вершинами графа существует единственный путь, граф является связным и не содержит циклов.

* * *

ДЕРЕВЬЯ И ВЕРОЯТНОСТИ

При анализе вероятностей различных событий (например, в играх) возможные альтернативные исходы и соответствующие вероятности часто представляют в форме дерева, где вершины соответствуют возможным исходам, а ребра — значениям вероятностей возможных исходов. Соответствующие расчеты выполняются на основе дерева. На рисунке представлено дерево, соответствующее игре, в которой нужно бросить сначала монету, затем — кубик. В теории игр, которая широко применяется в экономике, подобные представления используют очень часто.

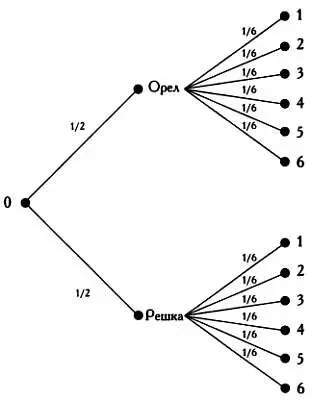
Для расчета вероятностей нужно четко представлять все возможные исходы.

* * *

У. УИНГФИЛД И А. А. МАРКОВ : ТЕННИС И ТЕОРИЯ ГРАФОВ

Уолтер Уингфилд(1833–1912) запатентовал игру под названием теннис в феврале 1874 года. Андрей Андреевич Марков(1856–1922) занимался изучением последовательностей случайных событий, которые позднее стали называться цепями Маркова. Цепь Маркова представляет собой ориентированный граф, вершинам которого соответствуют состояния, а дугам — переходы из одного состояния в другое в зависимости от вероятности исходного события, но не всей последовательности предшествующих событий. Уингфилда и Маркова объединяет работа А. Л. Садовского и Л. Е. Садовского «Математика и спорт», в которой цепи Маркова используются для анализа теннисных партий. Так, на рисунке вероятности возможных исходов для каждого события соответственно равны 0,6 и 0,4.

* * *

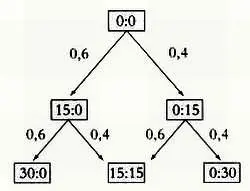
Рассмотрим задачу, которую можно решить с помощью деревьев. Даны n городов A 1, А 2 … А n . Зная затраты на установление сообщения между каждой парой городов (стоимость строительства дорог, прокладки водо- и газопровода, линий электропередачи, телефонных линий), определите, как можно соединить города самым дешевым способом. Очевидно, что сеть «экономических связей» будет деревом, так как все города должны быть связаны друг с другом и не должно существовать циклов. Если бы в этой сети существовал цикл, можно было бы удалить одно из его ребер и все города по-прежнему были бы соединены между собой, но уже при меньших затратах.