Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

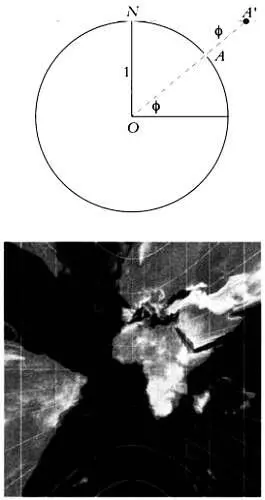
Схема центральной, или гномонической, проекции и карта, выполненная в этой проекции (центр проекции расположен на экваторе).

Это очевидно геометрическая проекция. Если мы вновь представим Землю как шар из полупрозрачного пластика, на поверхности которого нарисованы континенты, то сможем увидеть его гномоническую проекцию, если поставим шар на белый стол и разместим в центре шара точечный источник света.

Если точкой касания шара и плоскости является один из полюсов, то меридианы отображаются в виде радиальных равномерно распределенных прямых, исходящих из центра карты, где будет изображен полюс. Экватор в этом случае бесконечно удален, и его нельзя представить на карте. На такой бесконечной карте нельзя изобразить и полушарие целиком. Другие параллели будут иметь вид концентрических окружностей, центр которых совпадает с полюсом.

Карта, выполненная в полярной гномонической проекции. Центром проекции является Северный полюс.

Если точка касания шара и плоскости располагается на экваторе, то меридианы будут отображаться в виде параллельных прямых, распределенных неравномерно. Экватор в этой проекции будет выглядеть как прямая, перпендикулярная меридианам, а остальные параллели примут форму гипербол.

Если точкой касания шара и плоскости выбрать любую произвольную точку сферы, то меридианы будут изображаться в виде радиальных неравномерно распределенных прямых, указывающих на полюс. Экватор будет изображен в виде прямой, перпендикулярной только меридиану, проходящему через точку касания. Другие параллели, близкие к полюсу, примут форму эллипсов, параллель, проходящая через точку касания, будет изображена в виде параболы, остальные параллели — в виде гипербол.

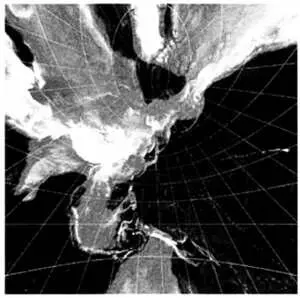
Карта, выполненная в косой гномонической проекции с центром в Японии.

Вот некоторые свойства карты в гномонической проекции.

1. Как правило, круглая форма (возможно, обрезанная тем или иным способом), карта охватывает лишь часть одного из полушарий.

2. Большие круги, проходящие через точку касания, отображаются как радиальные равномерно распределенные прямые (если мы рассмотрим несколько больших кругов, отстоящих друг от друга на равные углы), а точки, удаленные от точки касания на одинаковое расстояние, примут форму окружностей с центром в этой точке.

3. Форма и распределение меридианов и параллелей будут выглядеть так, как мы описали выше. Искажение в направлении меридианов будет равно μ = 1/sin 2 φ , в направлении параллелей — λ = 1/sin φ .

4. Гномоническая проекция сохраняет геодезические линии, но не сохраняет расстояния, площади и величины углов.

5. Искажение площадей, форм и углов, наименьшее в точке касания (в центре карты), будет увеличиваться по мере удаления от этой точки.

Доказать геометрическими методами, что гномоническая проекция сохраняет геодезические линии, очень просто. Геодезические линии сферы, большие круги, получаются сечением сферы плоскостью, проходящей через центр сферы. Следовательно, изображением большого круга в центральной проекции будет прямая, вдоль которой пересекаются плоскость, определяющая большой круг, и касательная плоскость, как показано на рисунке. Это доказывает, что гномоническая проекция преобразует геодезические линии сферы (ее большие круги) в геодезические линии плоскости (прямые).

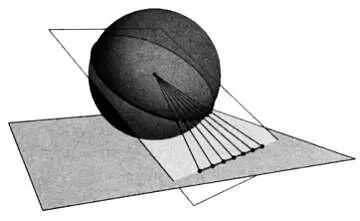
Гномоническая проекция сохраняет геодезические линии и преобразует большие круги сферы в прямые на плоскости.

Кроме того, можно доказать, что это по сути единственная картографическая проекция, обладающая подобным свойством. Если говорить о сохранении площадей или углов, то этим свойством обладает множество проекций.

Чтобы определить, сохраняет ли гномоническая проекция площади и (или) углы, вычислим искажения, возникающие при ее использовании на меридианах и параллелях. Для этого построим индикатрису Тиссо для произвольной точки сферы, то есть рассмотрим окружность достаточно малого размера (в действительности она будет бесконечно малой, поэтому можно считать, что окружность располагается на плоскости, касающейся сферы в этой точке) и рассчитаем размеры эллипса, в который преобразуется эта окружность в гномонической проекции.