Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

Это лишь немногие примеры пропагандистского использования карт, которые хранит история картографии.

Центральная, или гномоническая, проекция считается самой древней. Ее авторство обычно приписывается Фалесу Милетскому, который, как считается, использовал косую гномоническую проекцию для создания карт звездного неба. Эта азимутальная проекция земного шара на касающуюся его плоскость в древности называлась horologium («часы») и «гороскоп», так как гномон был частью солнечных часов. В солнечных часах гномон располагается под наклоном и указывает на Северный полюс. Тень гномона указывает время в течение дня, когда Солнце движется по небу. Углы между делениями, обозначавшими часы, на циферблате солнечных часов, размеченном для определенной широты, равны углам между меридианами в гномонической проекции, центр которой располагается на этой же широте. При этом 15° долготы равносильны разнице во времени ровно в один час.

Происхождение термина «центральная проекция» неизвестно. Термин «гномическая проекция» первым использовал английский математик Уильям Эмерсон в 1749 году. Позднее, в 1836 году, британский математик Огастес де Морган ввел современный термин «гномоническая проекция». Богатство геометрических свойств этой проекции основано на том, что кривые, указывающие кратчайшие пути (то есть геодезические линии), также называемые ортодромами, изображаются прямыми. Слабое место этой проекции заключается в том, что по мере удаления от точки касания (центра карты) искажения сильно возрастают, что делает проекцию неудобной для составления карт мира. Однако ее можно использовать в других целях.

* * *

ФАЛЕС МИЛЕТСКИЙ (ОК. 624 ГОДА ДО Н. Э. — ОК. 547 ГОДА ДО Н. Э.)

О жизни и творчестве этого греческого философа и математика мало что известно. Сведения о нем дошли до нас благодаря работам более поздних философов и историков, в частности Аристотеля, Геродота и Диогена Лаэртского. Фалес, учитель Пифагора, считался первым философом Античности и первым из семи мудрецов Греции. Ему приписывается ряд геометрических открытий, два из которых объединены общим названием «теорема Фалеса».

1. Угол, вписанный в полуокружность, прямой.

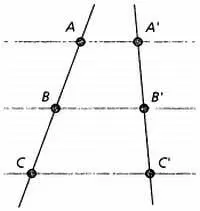
2. Если на одной из двух прямых отложить последовательно несколько пропорциональных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные между собой отрезки.

Хотя мы не можем точно утверждать, каков на самом деле был вклад Фалеса в науку, достоверно известно одно: он был первым математиком, которому присваивались конкретные математические открытия. Фалес считается создателем дедуктивной геометрии; различные источники приписывают ему авторство решений множества практических задач. Так, Фалес измерил размеры египетских пирамид по длине их тени с помощью вертикально расположенной палки, предсказал солнечные затмения и вычислил расстояние от корабля до берега с помощью подобия треугольников. Благодаря Аристотелю нам известно, как Фалесу удалось разбогатеть. Ученый, применив знания астрономии, предсказал высокий урожай оливок и взял под контроль маслобойни в Милете и на Хиосе. Несколько месяцев спустя, когда урожай был собран, Фалес смог диктовать покупателям свои цены. В результате он разбогател и посрамил всех, кто попрекал его бедностью и называл его философию бесполезной.

* * *

Рассмотрим сферу и касательную ей плоскость. Отображением точки А на поверхности сферы, полученным с помощью центральной проекции, будет точка А' на плоскости, определяемая как пересечение прямой, проходящей через точку А и центр сферы, с этой плоскостью.