Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

квадратную сетку (расстояния между ними одинаковы). Математическая формулировка этой проекции проще, так как всего лишь представляет на плоскости широту φ и долготу θ . Цилиндрическая проекция Миллера была создана в 1942 году в попытках сохранить внешний вид проекции Меркатора и уменьшить искажения у полюсов, однако она не является ни равновеликой, ни конформной, то есть не сохраняет ни площади, ни углы. О проекции Меркатора мы подробно расскажем в главе 9.

На рисунке вы можете видеть, как распределяются параллели в Северном полушарии при использовании разных цилиндрических проекций с одинаковым масштабом у экватора, и оценить вносимые искажения.

Сравнение расположения параллелей в некоторых цилиндрических проекциях.

Кроме того, можно рассмотреть разновидности картографических проекций (прямые, поперечные и косые), которые отличаются расположением плоскости, цилиндра или конуса проекции относительно земной сферы. В этих проекциях сетка меридианов и параллелей выглядит по-разному. Прямые цилиндрические проекции (геометрические и алгоритмические) — это проекции, в которых цилиндр касается сферы на экваторе или рассекает ее вдоль двух параллелей — этот случай мы рассмотрели выше. В поперечных цилиндрических проекциях цилиндр касается меридиана или рассекает сферу вдоль окружностей, параллельных меридиану. В косой проекции точки касания расположены на большом круге, который не является ни меридианом, ни экватором, либо линии пересечения цилиндра и сферы являются окружностями, параллельными большому кругу сферы. Поперечные и косые цилиндрические проекции удобно использовать, когда необходимо заострить внимание на какой-либо области, расположенной вдоль меридиана, так как искажение вблизи линий касания цилиндра и сферы меньше.

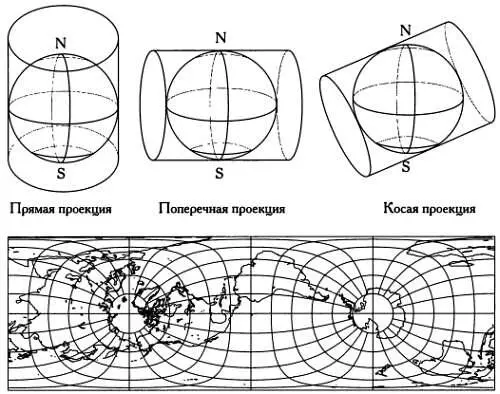
На схемах вверху представлены различные цилиндрические проекции. На рисунке снизу изображена равновеликая цилиндрическая поперечная проекция Ламбертас касательным меридианом 90° западной долготы, пересекающим Северную Америку с севера на юг.

Прямые цилиндрические проекции сильно искажают формы и очень часто искажают площади участков вблизи полюсов. Прямоугольные карты мира, составленные с помощью этих проекций, рисуют нам неверную картину мира.

В псевдоцилиндрических проекциях предпринята попытка решить эти проблемы путем сближения параллелей по мере приближения к полюсам. Прямые псевдоцилиндрические проекции, в которых линия касания сферы и цилиндра проходит по экватору, обладают следующими свойствами.

1. Параллели изображаются горизонтальными прямыми, необязательно равноудаленными друг от друга.

2. Меридианы изображаются произвольными кривыми, отстоящими друг от друга на одинаковое расстояние вдоль каждой параллели.

Следовательно, как и в цилиндрических проекциях, масштаб псевдоцилиндрических проекций вдоль параллелей постоянен. Но так как меридианы и параллели пересекаются не под прямым углом, ни одна из таких проекций не может быть конформной. В атласах часто используются две равновеликие проекции: проекция Моллвейде (в 1805 году в этой проекции была выполнена эллиптическая карта мира, на которой меридианы имеют форму эллипсов) и синусоидальная проекция Сансона — Флемстида (возможно, первым ее использовал Меркатор), в которой меридианы изображаются синусоидальными кривыми. В псевдоцилиндрических проекциях также были составлены карта Колиньона (1865; в вариантах этой карты, имеющих форму треугольника и ромба, меридианы изображены наклонными прямыми. Эти карты сохраняют площади, но очень сильно искажают формы), шесть карт Эккерта (1906; карты с четными номерами являются равновеликими, в картах с нечетными номерами параллели равноудалены друг от друга, в первой паре карт меридианы изображены прямыми, во второй паре — окружностями, в третьей паре — эллипсами) и карта в проекции Робинсона (1974; эта проекция используется при составлении карт мира Национальным географическим обществом вместо проекции Меркатора).

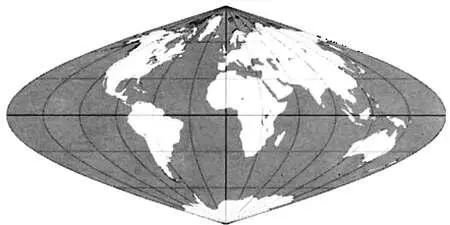
Карта мира, выполненная в синусоидальной проекции, или проекции Сансона— Флемстида. Эта проекция также известна как равновеликая проекция Меркатора, так как Меркаториспользовал ее в некоторых своих картах.