Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

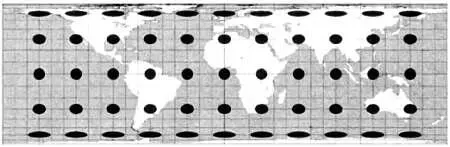
Индикатриса Тиссо, или эллипс искажения — один из способов графического изображения искажений на карте. В разных участках земной поверхности строятся небольшие окружности, после чего по их проекциям на карте можно увидеть проективные искажения в различных участках карты. Так, если мы примем радиус окружности равным λ, она преобразуется в эллипс, длины полуосей которого будут равны λи μ. Если λ = μ, то эллипсы примут форму окружностей, а отображение будет конформным. При λ= 1/ μотображение будет равновеликим. На иллюстрации представлена индикатриса Тиссо для равновеликой цилиндрической проекции Ламберта.

Наконец, очевидно, что эта проекция не сохраняет геодезические линии, за исключением меридианов и экватора. Вывод таков: равновеликие проекции могут не быть изометрическими, и одного лишь сохранения площадей для создания точной карты Земли недостаточно.

Равновеликая цилиндрическая проекция Ламберта — это геометрическая цилиндрическая проекция, определяемая как геометрическая проекция земной сферы на касающийся ее цилиндр (как правило, точки касания лежат на экваторе) с последующим развертыванием цилиндра на плоскости (для этого цилиндр разрезается вдоль одного из меридианов, то есть вертикально). В картах, созданных с использованием этой проекции, искажения возникают на первом этапе построения, так как развертывание цилиндра на плоскость является изометрическим преобразованием и не искажает размеры. Если изменить диаметр основания цилиндра, то есть уменьшить его так, чтобы он рассекал сферу, или же сменить его положение либо проекцию лучей, то мы получим различные геометрические цилиндрические проекции.

Другими проекциями этого же типа являются центральная цилиндрическая проекция и стереографическая проекция Брауна. В центральной цилиндрической проекции «лучи света» распространяются из центра сферы на ее поверхность и на поверхность цилиндра. Искажения у полюсов, вносимые этой проекцией, очень велики и даже больше, чем искажения в проекции Меркатора. В стереографической проекции Брауна, разработанной в 1867 году, центром проекции для произвольной точки меридиана служит противолежащая точка экватора на этом же меридиане.

Эта проекция, как и в свое время стереографическая проекция Галла, была создана в попытках устранить излишние искажения у полюсов, возникающие при использовании проекции Меркатора.

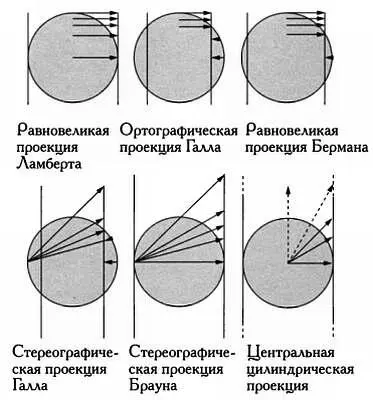
Сечения для некоторых геометрических цилиндрических проекций, показывающие разницу размеров и внешнего вида карт, созданных с использованием этих проекций.

Мы считаем, что цилиндр касается сферы на экваторе, но также можем рассмотреть случаи, когда цилиндр рассекает сферу вдоль двух параллелей, симметричных относительно экватора. Так, если цилиндр рассекает сферу вдоль параллелей 30° с. ш. и ю. ш., то равновеликая цилиндрическая проекция Ламберта станет эквивалентна проекции Бермана (1910) или проекции Галла — Петерса (1833 и 1967), если цилиндр рассекает сферу вдоль параллелей 45° с. ш. и ю. ш. Если в стереографической проекции Брауна цилиндр рассекает сферу вдоль 45-х параллелей, имеем стереографическую проекцию Галла (1885).

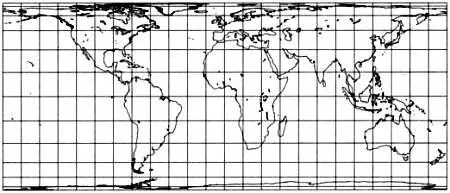
Карта, выполненная в равновеликой цилиндрической проекции Бермана, при которой цилиндр рассекает сферу вдоль 30-х параллелей.

Понятие цилиндрической проекции охватывает не только геометрические, но и алгоритмические проекции, которые обладают некоторыми общими свойствами с описанным выше геометрическими проекциями.

1. Линии координатной сетки, то есть меридианы и параллели, являются прямыми и перпендикулярны друг другу.

2. Масштаб вдоль каждой параллели постоянен (для разных параллелей он отличается), следовательно, меридианы равноудалены друг от друга. Длины всех меридианов и всех параллелей одинаковы.

Карты мира, созданные с помощью этих проекций, прямоугольные, а их метрические свойства симметричны относительно экватора. В качестве примеров можно привести цилиндрическую равнопромежуточную проекцию, цилиндрическую проекцию Миллера и проекцию Меркатора. В простой цилиндрической равнопромежуточной проекции, которую ввел Эратосфен, масштаб карты неизменен вдоль каждого меридиана, следовательно, параллели равноудалены друг от друга. Частным случаем является plate саrréе — проекция, в которой меридианы и параллели образуют