Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

* * *

В следующих главах мы продемонстрируем некоторые конкретные примеры конформных и равновеликих проекций, а также проекций, сохраняющих геодезические линии, и увидим, как они изменяют различные метрические свойства. Так мы сможем определить, существует ли проекция, позволяющая составить точную карту Земли, а также рассмотрим три примера известных старинных карт мира, сохраняющих углы, площади и кратчайшие пути. В частности, вы познакомитесь с проекцией Архимеда, сохраняющей площади, центральной, или гномонической проекцией, сохраняющей геодезические линии, и стереографической проекцией, сохраняющей углы. Однако ни одна из этих трех проекций не является изометрической. Как следствие, мы не сможем ограничиться рассмотрением исключительно конформных проекций (равновеликих проекций или проекций, сохраняющих геодезические линии).

* * *

ГЕОМЕТРИЧЕСКИЕ И АЛГОРИТМИЧЕСКИЕ ПРОЕКЦИИ

В основе первой классификации картографических проекций лежит метод их построения. По этому признаку проекции можно разделить на геометрические и алгоритмические («искусственные», аналитические или математические). Геометрические проекции — это проекции, которые с геометрической точки зрения можно интерпретировать как лучи света, которые исходят из точки, бесконечно удаленного источника или прямой и освещают Землю (ее можно представить как прозрачный пластиковый шар, на поверхности которого изображены континенты) согласно законам перспективы. Результатом этих проекций является изображение на плоской или промежуточной поверхности, например на поверхности цилиндра или конуса, которые затем разворачиваются на плоскости.

Геометрические проекции можно разделить на классы в зависимости от формы поверхности: это может быть плоскость, поверхность цилиндра или конуса. Такие проекции называются азимутальными, цилиндрическими и коническими соответственно. В качестве примеров геометрических проекций можно привести гномоническую, стереографическую, равновеликую цилиндрическую проекцию Ламберта или равновеликую коническую проекцию Альберса.

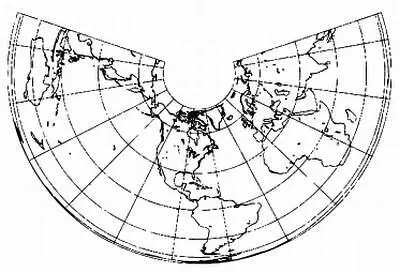
Карта, выполненная в равновеликой конической проекции Альберса(1805). Это геометрическая проекция, получаемая при проецировании сферической модели Земли на поверхность конуса, которая затем разворачивается на плоскости.

Тем не менее многие картографические проекции не имеют прямой геометрической трактовки и описываются с помощью математических формул, — они называются алгоритмическими. Среди них выделяются те, что основаны на принципах геометрии или являются производными от них, как, например, проекция Меркатора или Хаммера — Айтоффа. Существуют и чисто алгоритмические проекции, в числе которых выделяются знаменитые проекции Моллвейде, синусоидальная проекция Сансона — Флемстида, проекция Робинсона и тройная проекция Винкеля.

Деление на подклассы в зависимости от используемой вспомогательной поверхности (это может быть плоскость, цилиндр или конус) проводится, главным образом, среди алгоритмических проекций.

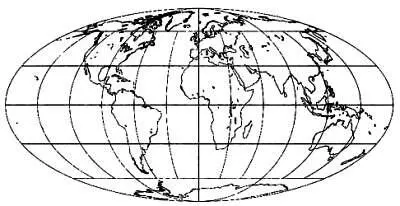
Карта, выполненная в проекции Моллвейде(1805). Это алгоритмическая проекция — она описывается чисто математическими выражениями. Она является равновеликой, в ней используется эллипс с соотношением длин осей 2:1. Параллели в этой проекции изображаются параллельными линиями.

ОРТОФОТОГРАФИЯ

При составлении небольших культурных или туристических карт городов очень часто используется ортофотография. При взгляде на ортофотографии большинство людей думают, что эти фото сделаны с самолета или спутника, то есть представляют собой карту в вертикальной перспективной проекции. Но это не совсем так. Ортофотография — это фотографическое изображение города, полученное из нескольких фотографий, сделанных с воздуха и скорректированных так, чтобы итоговое изображение соответствовало ортогональной проекции. Эта проекция строится с использованием параллельных лучей, идущих в одном направлении, и ее можно считать частным случаем вертикальной перспективной проекции, фокус которой расположен на бесконечности. Именно благодаря использованию ортогональной проекции при совмещении нескольких фотографий не возникает искажений.