* * *
ТОПОЛОГИЧЕСКИЕ КАРТЫ
Если мы нарисуем карту нашего дома, квартала или района, на ней не будет сохранен ни один из привычных параметров. Точно такими же были первые карты, созданные человеком, например вавилонская карта VI века до н. э., изображенная на глиняной табличке. Это так называемые топологические карты, на которых основное значение имеют отношения вида «близко — далеко», «вместе — раздельно», а также порядок и непрерывность. На топологических картах обычно изображают взаимосвязи между элементами местности. Хрестоматийным примером таких карт служат схемы метро, так как для тех, кто ими пользуется, важнее не расстояние между станциями, а их число и схемы пересадок.
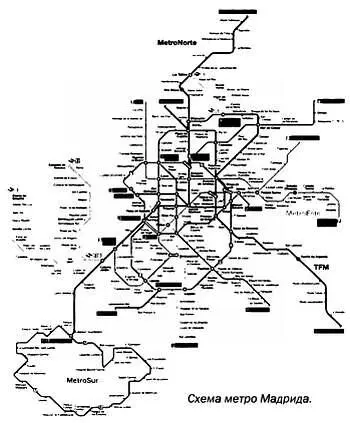
К топологическим картам относятся так называемые фэнтези-карты вымышленных миров, например карта Средиземья из «Властелина колец» Дж. Р. Р. Толкиена(1954) или «живописные карты», которые можно увидеть, например, в парках аттракционов. К этому же виду относятся карты нейронных сетей и другие карты, используемые в информатике, а также карты, связанные с графами.
* * *
Описанная выше сферическая модель Земли — это идеальная модель земной поверхности, которая отличается от нее только размером, но не формой. Масштаб указывает разницу в размерах между Землей и сферой. Определить его можно, разделив радиус сферы на радиус Земли. Рассмотрим глобус радиусом 25 см. Радиус Земли будем считать равным 6371 км (если использовать размеры эллипсоида WGS84). В этом случае масштаб равен

Этот масштаб, который обычно записывается как 1:25484000, означает, что каждый сантиметр глобуса соответствует 25484000 см, то есть 254,84 км земной поверхности.
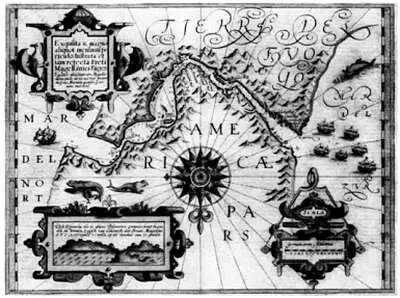
На многих древних картах масштаб указывался с помощью изображения компаса, как можно видеть на этой карте Магелланова пролива (1606), выполненной Йодокусом Хондиусом. На карте изображены и другие типичные элементы карт того времени, в частности роза ветров и фантастические животные.
Как влияет это уменьшение в размерах на метрические параметры карт, о которых мы говорили выше? Расстояния и длины кривых уменьшаются линейно в соответствии с масштабом, то есть каждый сантиметр глобуса соответствует 254,84 км земной поверхности. Следовательно, если мы хотим измерить расстояние от Барселоны до Аделаиды, нужно всего лишь измерить это расстояние на сферической модели Земли и умножить результат в сантиметрах на 254,84. Площади участков земной поверхности и масштаб карты связаны квадратичной зависимостью: каждый квадратный сантиметр на глобусе будет соответствовать 254,84 2= 64943,4256 км 2.
Большие круги, указывающие кратчайшие пути, станут большими кругами на сферической модели, поэтому геодезические линии также останутся неизменными. Сохранятся также углы и направления. Как видим, преобразование, которое заключается в уменьшении размеров Земли, не изменяет метрические параметры, масштаб во всех точках сферической модели остается постоянным.
Математически это можно выразить следующим образом. Будем считать, что Земля и ее сферическая модель имеют общий центр, который мы примем за начало нашего трехмерного пространства 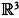 . Следовательно, наше математическое преобразование будет отображением Земли ( S 1 ), которая является сферой радиуса 6371 км, на сферическую модель ( S 2 ) радиусом 25 см φ: S 1 —> S 2 , определяемым как φ( х ) = е · х . На языке геометрии это отображение называется гомотетией (при е > 1 исходные фигуры увеличиваются, при е < 1, как в нашем случае, — уменьшаются). Это простое преобразование, которое однозначно определяется свойством пропорционального уменьшения размеров фигур.
. Следовательно, наше математическое преобразование будет отображением Земли ( S 1 ), которая является сферой радиуса 6371 км, на сферическую модель ( S 2 ) радиусом 25 см φ: S 1 —> S 2 , определяемым как φ( х ) = е · х . На языке геометрии это отображение называется гомотетией (при е > 1 исходные фигуры увеличиваются, при е < 1, как в нашем случае, — уменьшаются). Это простое преобразование, которое однозначно определяется свойством пропорционального уменьшения размеров фигур.
Теперь, когда вопрос об изменении размеров решен, осталось решить проблему изменения формы. Как вы увидите, она намного сложнее, и именно здесь в действительности скрывается святой Грааль картографии — идеальная карта. Чтобы решить эту проблему, нужно изучить математические проекции сферы на плоскость и рассмотреть, как они изменяют различные метрические свойства. Это центральная тема математической картографии и настоящей главы. Как мы упоминали в предисловии, существует множество математических преобразований сферы в плоскость и, как следствие, множество разных проекций, на основе которых можно составить столь же большое число самых разных карт. Далее для простоты мы будем понимать картографические проекции как отображения сферы единичного радиуса на плоскость 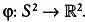 Кроме того, с математической точки зрения проекции должны обладать некоторыми естественными свойствами: в частности, они должны быть непрерывными и дифференцируемыми. Это означает, что сфера должна проецироваться на плоскость разумным образом, то есть без складок, разрезов и наложений.
Кроме того, с математической точки зрения проекции должны обладать некоторыми естественными свойствами: в частности, они должны быть непрерывными и дифференцируемыми. Это означает, что сфера должна проецироваться на плоскость разумным образом, то есть без складок, разрезов и наложений.
Читать дальше




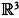 . Следовательно, наше математическое преобразование будет отображением Земли ( S 1 ), которая является сферой радиуса 6371 км, на сферическую модель ( S 2 ) радиусом 25 см φ: S 1 —> S 2 , определяемым как φ( х ) = е · х . На языке геометрии это отображение называется гомотетией (при е > 1 исходные фигуры увеличиваются, при е < 1, как в нашем случае, — уменьшаются). Это простое преобразование, которое однозначно определяется свойством пропорционального уменьшения размеров фигур.
. Следовательно, наше математическое преобразование будет отображением Земли ( S 1 ), которая является сферой радиуса 6371 км, на сферическую модель ( S 2 ) радиусом 25 см φ: S 1 —> S 2 , определяемым как φ( х ) = е · х . На языке геометрии это отображение называется гомотетией (при е > 1 исходные фигуры увеличиваются, при е < 1, как в нашем случае, — уменьшаются). Это простое преобразование, которое однозначно определяется свойством пропорционального уменьшения размеров фигур.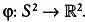 Кроме того, с математической точки зрения проекции должны обладать некоторыми естественными свойствами: в частности, они должны быть непрерывными и дифференцируемыми. Это означает, что сфера должна проецироваться на плоскость разумным образом, то есть без складок, разрезов и наложений.
Кроме того, с математической точки зрения проекции должны обладать некоторыми естественными свойствами: в частности, они должны быть непрерывными и дифференцируемыми. Это означает, что сфера должна проецироваться на плоскость разумным образом, то есть без складок, разрезов и наложений.










