Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

Как мы уже отмечали, важно знать, как изменяются основные метрические свойства при использовании тех или иных проекций. Поэтому начнем наши поиски точной карты земной сферы с того, что докажем следующее утверждение: в проекции, сохраняющей расстояния между точками (такие отображения называются изометрическими), также сохраняются кратчайшие пути (геодезические линии), углы и площади. Кроме того, сохранение расстояний эквивалентно сохранению длин кривых. Предыдущие утверждения — не более чем частный случай анализа дифференцируемых отображений между регулярными поверхностями применительно к их метрическим свойствам (доказательство этого утверждения методами дифференциальной геометрии можно найти в любом классическом учебнике по этой дисциплине).

Далее мы докажем, что любая проекция сферы на плоскость, сохраняющая расстояния (это означает, что расстояние между двумя произвольными точками сферы будет равно расстоянию между отображениями этих точек на плоскости), также сохраняет кратчайшие пути, иными словами, отображением больших кругов сферы будут прямые на плоскости.

Докажем это утверждение методом от противного, который заключается в том, что мы считаем утверждение, которое хотим доказать, ложным, и путем логических рассуждений приходим к противоречию, затрагивающему исходную гипотезу. Следовательно, утверждение, которое мы хотим доказать, будет истинным. В нашем случае предположим, что проекцией больших кругов не всегда будет прямая.

Если бы рассматриваемая проекция в самом деле не сохраняла кратчайшие пути, то существовали бы две точки сферы А и В и точка С , лежащая на кратчайшем пути между ними (то есть на большом круге, проходящем через А и В ), такая, что ее отображение на плоскость С' не лежало бы на кратчайшем пути (прямой), соединяющем отображения точек А и В — А' и В' соответственно.

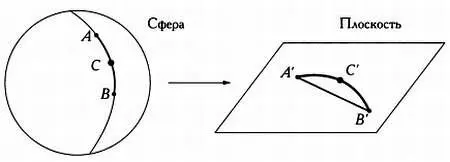
Имеем: так как рассматриваемая проекция сохраняет расстояния, то расстояние между отображениями А' и В' равно расстоянию между исходными точками А и В :

d( A, B ) = d( A', B' ).

Так как точка С лежит на кратчайшем пути между А и В , расстояние между этими точками будет равно сумме расстояний между А и С и между С и В :

d( A, B ) = d( A, C ) + d( C, B ).

Тем не менее точка С не лежит на прямой, соединяющей А' и В' , следовательно:

d( A', B' ) < d( A', C' ) + d( C', B' ).

Но так как рассматриваемая проекция сохраняет расстояния, то последняя сумма будет равна d( A, С ) + d( С, В ). Имеем противоречие: мы доказали, что

d( A, B ) < d( A, B ).

Это очевидно ложное утверждение означает, что проекция не сохраняет кратчайшие пути.

Используем утверждение из предыдущего раздела (проекции, сохраняющие расстояния, сохраняют и кратчайшие пути), чтобы доказать, что в этом случае кривые на сфере преобразуются в кривые на плоскости, имеющие ту же длину. Почему это утверждение верно? Во-первых, любую кривую на сфере можно приближенно представить в виде конечного (но достаточно большого) числа дуг больших кругов. Концы этих дуг р 0, р 1, р 2 , …, р n-1, p n лежат на кривой, как показано на иллюстрации.

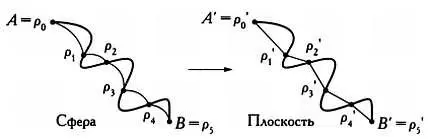
Следовательно, длину кривой можно приближенно представить как сумму длин этих дуг, или, иными словами, как сумму расстояний между их концами. Так как речь идет о дугах больших кругов, это будут кратчайшие расстояния, соединяющие концы дуг:

l( α ) = d( р 0 , р 1 ) + d( р 1 , p 2 ) + …+ d( р n-1 , р n ).

Во-вторых, кривую на плоскости, которая является отображением исходной кривой на сфере, можно приближенно представить с помощью множества отрезков, которые будут отображениями дуг больших кругов (об этом мы рассказали в прошлом разделе), а длину плоской кривой — как сумму длин расстояний между концами этих отрезков р' 0 , р' α , р' 2 , …, p' n :