Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

Натянутая веревка соответствует кратчайшему пути между двумя точками.

На интуитивном уровне можно сформулировать следующее доказательство. Допустим, даны две точки на сфере, и мы хотим найти кривую, которая определяет кратчайший путь между ними. Кажется логичным предположить, что мы можем ограничиться рассмотрением окружностей сферы, которые проходят через эти точки и образуются сечением сферы плоскостями, проходящими через две данные точки. Кроме того, в силу свойств симметрии, четко видно, что дуга окружности, полученной сечением сферы плоскостью, проходящей через центр сферы, соответствует кратчайшему пути между точками, что показано на предыдущем рисунке. В итоге большие круги являются геодезическими линиями сферы, или кривыми, указывающими наименьшее расстояние.

Дуга большого круга, заключенная между между двумя точками, имеет наименьшую длину среди всех дуг окружностей, соединяющих данные точки.

* * *

ГЕОДЕЗИЧЕСКИЕ КУПОЛА

Одно из самых впечатляющих сооружений сферической формы, созданных в XX веке, — это геодезические купола Ричарда Бакминстера Фуллера(1895–1983). Мы могли бы многое сказать об этом гениальном изобретателе, архитекторе, инженере, математике, поэте и космологе, провидце, который опередил свое время и смог поставить науку и технику на службу обществу. Величайшим его творением, несомненно, являются геодезические купола.

Американский павильон на Всемирной выставке 1967 года в Монреале, построенный по проекту Ричарда Бакминстера Фуллера. Позднее в павильоне разместился музей воды и окружающей среды

(фотография: Филипп Хайнсторфер).

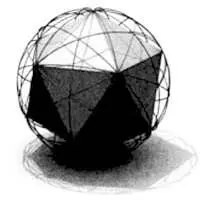
Геодезический купол — это сферическая структура, образованная сеткой больших кругов (геодезических линий). Треугольники, из которых состоит сетка, придают структуре жесткость. Для построения классического геодезического купола рассматривается икосаэдр, вписанный в сферу, как показано на иллюстрации. Затем каждая грань икосаэдра делится на треугольники, которые проецируются на сферу, образуя сетку геодезических линий.

Преимущества геодезического купола следующие.

1. Он покрывает обширное пространство и не требует поддерживающих конструкций в середине.

2. Для геодезического купола характерно оптимальное соотношение объема к площади поверхности, иными словами, он покрывает пространство максимального объема при наименьшей площади поверхности.

3. Пространство внутри купола нетрудно обогревать, так как потери тепла зависят от соотношения между объемом и площадью поверхности, которое является оптимальным.

4. Геодезические купола благодаря своей структуре и распределению нагрузки обладают высокой жесткостью.

5. Геодезические купола имеют малый вес и просты в сборке.

* * *

Прямые также можно определить как кривые, обладающие нулевой кривизной. Можно ли дать похожее определение большим кругам сферы? Кажется очевидным, что окружность, будучи плоской кривой, имеет одинаковую кривизну во всех точках, и эта кривизна ненулевая. Кроме того, чем больше радиус окружности, тем более вытянутой она будет, и тем меньше будет ее кривизна (см. иллюстрацию на следующей странице). Геометрически кривизна окружности радиуса r равна 1/ r . Следовательно, чем больше радиус окружности, тем меньше ее кривизна. Изменение кривизны окружности в зависимости от ее радиуса можно почувствовать, если проехать на велосипеде по кругу: в зависимости от радиуса круга нужно будет поворачивать руль на больший или меньший угол. Когда мы не поворачиваем руль, велосипед движется по «прямой», то есть по большому кругу, имеющему наименьшую кривизну. Следовательно, большие круги имеют наименьшую кривизну, а их радиус будет наибольшим.

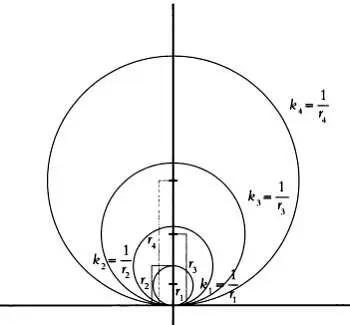
Чем больше радиус окружности r, тем меньше ее кривизна k.