Антонио Дуран - Том 27. Поэзия чисел. Прекрасное и математика

Фрагмент одной из скульптур в галерее романского аббатства в Мильштадте, Австрия, построенного в X веке.

Та же самая история искусства объясняет, почему скульпторы вернулись к классическому канону и почему фигуры мужчины и женщины вновь стали привлекать основное внимание художников. История искусства также помогает выделить различия между классической скульптурой и скульптурой более поздних периодов, вплоть до романтического неоклассицизма.

Давид работы Микеланджело(1501–1504) и Венера работы Антонио Пановы(1804–1812).

И наконец, чтобы лучше оценить красоту новых форм, которые с возвращением к классическому реализму начали проявляться в скульптуре, необходимо знать, какие новые цели ставили перед собой художники. История искусства показывает, как скульпторы уходили от холодного совершенства и создавали произведения, более впечатляющие зрителя. Как можно понять ускорение развития искусства в последние 150 лет, если не знать его историю? Можно ли оценить эстетику скульптуры «Поцелуй» Константина Бранкузи — варианта одноименной работы его учителя, Огюста Родена, не зная истории, которая объясняет этот возврат к палеолитическим истокам (см. иллюстрацию на следующей странице)?

«Поцелуй» Огюста Родена(1889) и скульптура с одноименным названием авторства Константина Бранкузи, созданная в 1908 году.

Можно ли оценить красоту некоторых произведений последнего столетия, например знаменитого «Фонтана» Дюшана, не понимая эстетической ценности выхода за пределы дозволенного?

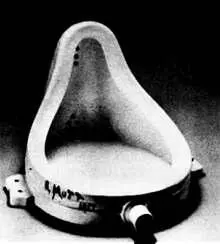
«Фонтан» (1917) — самый известный «реди-мейд» Марселя Дюшана. Как вы можете видеть на фотографии, скульптура не подписана именем Дюшана. Художник, доводя абсурдную идею до конца, подписался именем немецкого производителя унитазов — R. Mutt.

* * *

ДЮШАН И «РЕДИ-МЕЙДЫ»

Марсель Дюшан своими «реди-мейдами» («готовыми вещами») выразил следующую идею: любой предмет может стать произведением искусства, если так решил художник. Это был революционный жест, удар в самое сердце искусства. Дюшан, который интересовался математикой, физикой и в особенности шахматами, посвятил много времени поискам ответа на вопрос, тесно связанный с эстетической ценностью математики: можно ли создать в уме произведения искусства, не основанные на результатах зрительного восприятия?

Марсель Дюшанв образе Розы Селяви. Фотография Мана Рэя, 1921 год.

* * *

История математики поможет понять эстетическую ценность математических рассуждений подобно тому, как история искусства помогает понять эстетику скульптуры. Учитывая, что оценить красоту математики намного сложнее (и об этом мы уже говорили), роль истории в решении этой задачи также намного важнее, чем при эстетическом восприятии любого направления искусства.

Рассмотрим, например, высказывание: любой треугольник, вписанный в полуокружность, — прямоугольный. Диоген Лаэртский, основываясь на вторичных источниках, приписывает авторство этой теоремы Фалесу, который в благодарность за ее открытие принес в жертву буйвола. По мнению Диогена, Фалес был и автором доказательства этой теоремы, однако Аполлодор, опираясь на, возможно, более авторитетные источники, считает автором этой теоремы Пифагора.

Эту на первый взгляд простую теорему можно доказать несколькими способами. Однако истинный ключ к ней дает история математики: теорема Фалеса стала одной из первых сопровождавшихся рассуждениями, целью которых было подтвердить правильность теоремы в общем случае. Иными словами, теорема сопровождалась доказательством в его классическом понимании. Доказательство — не более чем логическое рассечение утверждения на ряд универсальных и очевидных истин. Чтобы понять всю важность этого первого в истории доказательства, теорему Фалеса нужно сравнить с математическими рассуждениями древних египтян или жителей Месопотамии, то есть вновь обратиться к истории математики. Если мы будем знать контекст той эпохи, теорема Фалеса уже не покажется нам столь примитивной. Мы даже сможем почувствовать, насколько концептуально близкими были греки к некоторому примитивизму, который мы находим в математических рассуждениях египтян или вавилонян. Будет уместно привести фразу, которую Харди как-то сказал Литлвуду: «Греческие математики не были одаренными школьниками — они принадлежали к другому университету». Подобно Венере Виллендорфской, теорема Фалеса имеет историческую ценность, и знание этой ценности позволяет оценить ее с эстетической точки зрения.