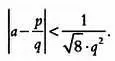Антонио Дуран - Том 27. Поэзия чисел. Прекрасное и математика

Уравнение Маркова

Диофантово уравнение, которое мы рассмотрим ниже, названо в честь русского математика Андрея Андреевича Маркова(1856–1922). Оно записывается так:

p 2+ q 2+ r 2= 3· p · q · r .

Натуральные числа, которые являются решениями этого уравнения (точнее, натуральные числа р , для которых существуют q и r такие, что р, q, r удовлетворяют уравнению), упорядоченные по возрастанию, называются числами Маркова. О них известно немало, но далеко не все. Так, известно, что чисел Маркова бесконечно много и что первые 16 членов ряда таковы:

1, 2, 5, 13, 29, 34, 89, 169, 194, 233, 433, 610, 985, 1325, 1597 и 2897.

Существует простой метод, позволяющий получить новые числа Маркова на основе уже известных. Нетрудно показать, что если p 1, q 1и r 1удовлетворяют уравнению Маркова и мы запишем р 2= 3· q 1 · r 1— р 1, q 2 = 3· p 1 · r 1— q 1 , и r 2 = 3· p 1 · q 1— r 1 , то тройка p 2, q 1 и r 1 также будет удовлетворять уравнению Маркова. Это же будет справедливо для троек р 1, р 2 и r 1 , а также p 1, q 1, r 2 .

Марков доказал, что все целые положительные решения уравнения Маркова можно получить с помощью этого простого метода, приняв в качестве начальных значений p 1 = 1, q 1 = 1 и r 1 = 1.

Живительно, что уравнение Маркова имеет великое множество решений. Но если его немного изменить, оно не будет иметь ни одного решения: к примеру, уравнение р 2+ q 2 + r 2= 2· р · q · r не имеет целых положительных решений. В действительности, как доказал Гурвиц, ни одно уравнение вида р 2+ q 2 + r 2= k · р · q · r не имеет целых положительных решений, за исключением случаев, когда k равно 3 (имеем уравнение Маркова), 1 или 0.

Решения уравнения Маркова р, q и r при р = 1 образуют первую связь с теоремой Гурвица о рациональном приближении. В самом деле, эти решения имеют вид р = 1, q = f 2n-1 и r = f 2n+1 , где f k — соответствующее число Фибоначчи. Первыми двумя числами Фибоначчи являются f 1 = 1 и f 2 = 1, каждое последующее число Фибоначчи определяется как сумма двух предыдущих. Имеем: f 3 = 1 + 1 = 2, f 4 = 3, f 5 = 5, f 6 = 8, f 7 = 13, f 8 = 21, f 9 = 34 и так далее. Числа Фибоначчи встречаются в природе столь же часто, что и золотое сечение, с которым они тесно связаны: если рассмотреть отношение двух последовательных чисел Фибоначчи, f n+1 / f n , то полученные дроби 2/1, 3/2, 5/3, 8/5, 13/8…, будут всё больше и больше приближаться к золотому числу. Приближение вновь будет описываться теоремой Гурвица:

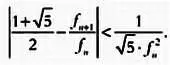
Это соотношение устанавливает неразрывную связь между числами Маркова и рациональным приближением. Очевидно, что эта связь намного прочнее.

Как мы уже отмечали, из-за золотого сечения рациональное приближение, описываемое теоремой Гурвица, нельзя улучшить. Это справедливо для золотого числа Ф и всех иррациональных чисел, эквивалентных ему с точки зрения рационального приближения. Иными словами, речь идет об иррациональных числах вида ( m · Ф + n )/( р · Ф + q ), где m, n, р, q — произвольные целые числа, которые удовлетворяют условию m·q — n · р = ± 1.

Математик Андрей Андреевич Марковсовершил важные открытия в теории чисел и теории вероятностей.

Оставим в стороне золотое сечение и все иррациональные числа, эквивалентные ему. Гурвиц доказал, что его теорема допускает более точную оценку, так как константу 1/√5 можно заменить другой, меньшей константой 1/√8: для произвольного иррационального числа а , за исключением золотого числа и эквивалентных ему, существует бесконечное множество дробей p / q таких, что

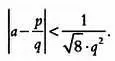
Это приближение нельзя улучшить: если принять а = √2, то его рациональное приближение не может быть точнее, чем допускает константа 1/√8, умноженная на число, обратное квадрату знаменателя.

Однако если мы оставим в стороне √2 и все эквивалентные ему, то сможем еще больше улучшить рациональное приближение, заменив константу 1/√8 другой, меньшей константой 5/√221. Для любого иррационального числа а , за исключением золотого числа, квадратного корня из 2 и эквивалентных им, существует бесконечно много дробей вида p / q таких, что