Антонио Дуран - Том 27. Поэзия чисел. Прекрасное и математика

* * *

Каким бы монструозным нам ни казалось число

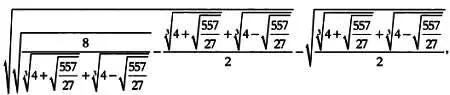
оно является алгебраическим, так как его можно представить как решение уравнения четвертой степени с целыми коэффициентами х 4+ 8 х — 5 = 0. Все числа, которые не являются алгебраическими, в математике называются трансцендентными. В некотором смысле они максимально далеки от натуральных чисел, которые мы используем при счете.

Самые знаменитые математические константы — обычно трансцендентные числа. Так, трансцендентными являются число π и число е , однако это было доказано лишь в конце XIX века. Трансцендентность числа π имеет удивительное следствие: задача о квадратуре круга не имеет решения. Иными словами, с помощью циркуля и линейки нельзя построить квадрат, равный по площади данному кругу. Задача о квадратуре круга не давала покоя древнегреческим математикам, однако ее решение было найдено лишь в конце XIX столетия. Если мы сравним решение математической задачи с установлением мирового рекорда, то задача о квадратуре круга стала рекордом, который не удавалось превзойти две с половиной тысячи лет!

При поиске приближения алгебраических чисел в виде дробей нельзя найти более точное приближение, чем описанное теоремой Дирихле. Если мы рассмотрим произвольное алгебраическое число а и число k , строго большее 2 ( k > 2), то, за некоторыми исключениями (число этих исключений всегда будет конечным), будет выполняться неравенство | а — р / q | > 1/ q k .

Это означает, что результат Дирихле нельзя улучшить относительно степени знаменателя. Однако с единицей, «сопровождающей» знаменатель, дело обстоит иначе. В 1891 году другой немецкий математик, Адольф Гурвиц, доказал, что эту константу можно заменить меньшей: 1/√5. Так, для произвольного иррационального числа а существует бесконечно много дробей вида p / q таких, что | а — p / q | < 1/(√5· q 2). Гурвиц также доказал, что значение 1/√5 является минимально возможным, поскольку существует еще одна математическая константа, так называемое золотое число, описывающее золотое сечение, Ф= (1 + √5)/2.

Адольф Гурвиц(1859–1919), один из величайших математиков XX столетия, внесший особый вклад в изучение алгебраических кривых и теорию чисел.

Золотое сечение — это соотношение сторон прямоугольника совершенных пропорций. Согласно древнегреческим геометрам, прямоугольник обладает совершенными пропорциями, если при отсечении от него квадрата со стороной, равной меньшей стороне прямоугольника, оставшийся прямоугольник будет иметь прежнее соотношение сторон. Допустим, длина короткой стороны прямоугольника равна а , длинной стороны — b . Следовательно, длины сторон нового прямоугольника будут равны b — а и а . Соотношение сторон прямоугольника будет наиболее гармоничным при b / а = а /( Ь — а ). Приняв х = b / а , имеем х = 1/( х — 1), то есть х 2— х — 1 = 0. Положительный корень этого уравнения равен золотому числу Ф = (1 + √5)/2.

Если мы отсечем от прямоугольника золотого сечения бесконечное число квадратов и будем соединять противоположные вершины этих квадратов дугами длиной в четверть окружности, получим спираль золотого сечения, изображенную ниже.

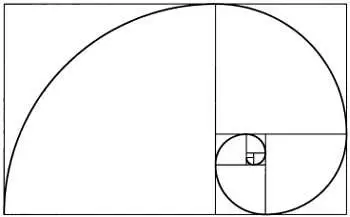
Именно такую форму имеет раковина наутилуса, в виде этой спирали располагаются семена подсолнуха, облака в ураганах и антициклонах и звезды во многих галактиках.

Форму золотой спирали имеют раковины наутилуса, ураганы и галактики.

Золотое сечение присутствует в природе повсеместно. Оно привлекало математиков, художников, архитекторов и музыкантов. Обратимся к творчеству Дюрера. Из всех художников Возрождения он, возможно, лучше всех разбирался в математике. Все, что Дюрер знал о возведении городских стен и крепостей, об использовании циркуля и угольника для измерения размеров твердых тел, о пропорциях человеческого тела и о форме букв алфавита, он изложил во множестве книг, напечатанных после его смерти. Большую часть математических знаний Дюрер получил в Италии. По рекомендации венецианского художника Якопо де Барбари он в 1506 году отправился в Болонью, где постигал тайную науку у неизвестного наставника. Многие считают, что этим учителем был монах-францисканец Лука Пачоли, который в 1494 году составил большую математическую энциклопедию XV столетия. До какой степени Дюрер проник в тайны изученной им науки, в которой золотое сечение было заветной формулой идеальных пропорций человеческого тела, можно судить по его прекрасным картинам, где изображены обнаженные Адам и Ева. Оцените разницу между головастым Адамом и пышнотелой Евой на гравюрах Дюрера 1504 года (сегодня они хранятся в венской галерее Альбертина) и ими же, прекрасными и стройными, на картинах 1507 года (они выставлены в мадридском музее Прадо).