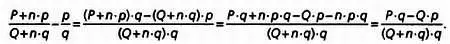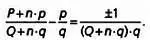Антонио Дуран - Том 27. Поэзия чисел. Прекрасное и математика

* * *

ПРОЖОРЛИВЫЕ ОКРУЖНОСТИ ФОРДА

Представленные ниже простые расчеты должны убедить читателя, что окружности Форда, касающиеся данной окружности, соответствующей дроби p/ q, неограниченно приближаются к точке, соответствующей этой дроби. Рассмотрим касающиеся окружности, расположенные слева от дроби p/ q. Они соответствуют дробям ( Р+ n· p)/( Q+ n· q), где n— любое натуральное число. Теперь достаточно показать, что разность между этими дробями и p/ qнеограниченно уменьшается с увеличением n:

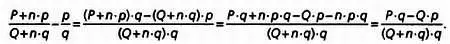
Так как окружности, соответствующие дробям p/ qи P/ Q, касаются, то, как мы отмечали выше, числа р· Qи Р· qбудут последовательными. Как следствие, их разность будет равна 1 или -1. С учетом этого предыдущее равенство примет вид:

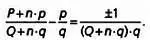
Так как nрасположено в знаменателе, то с его увеличением разность между p/ qи ( Р+ n· p)/( Q+ n· q) будет уменьшаться и в пределе, при бесконечно большом n, будет равна нулю.

* * *

Читатель согласится с тем, что окружности Форда настолько исполнены гармонии и элегантности, насколько отсутствие этих атрибутов характерно для доньи Росы; ее вздутого, как мех с оливковым маслом, живота, который Села называет «воплощением враждебности сытого к голодному».

Мартин Марко , или рациональное приближение иррациональных чисел

Оставим ненадолго донью Росу и окружности Форда и обратимся к биографии второго нашего героя — Мартина Марко, или рационального приближения иррациональных чисел.

Пифагор и пифагорейцы основывали математику и рациональное объяснение природы на том, что всю Вселенную можно свести к числам. Для пифагорейцев существовали только натуральные числа (1, 2, 3, 4, 5 и так далее) и дроби, которые можно было образовать из натуральных чисел. Тем не менее когда ученики Пифагора занялись простейшей геометрической операцией — измерением отрезков, основы их научной картины мира рухнули. Длина диагонали квадрата со стороной 1 оказалась в точности равна √2. Пифагорейцев постигло разочарование, когда они поняли, что √2 нельзя представить в виде дроби (об этом подробно рассказано на следующей странице). Что может быть проще, чем измерить диагональ квадрата? Однако даже ее нельзя точно выразить с помощью натуральных чисел и рациональных дробей. По легенде, Гиппас из Метапонта, пифагореец, раскрывший эту тайну кому-то из непосвященных, был сброшен в море с борта корабля и осужден вечно бороздить волны: «Раскрыв секрет невыразимого, он удостоился страшнейшего наказания — быть отделенным от сущего и низвергнутым в ничто, откуда прибыл».

Вскоре стало понятно, что, помимо чисел 1, 2, 3, 4, 5 и т. д., которые мы используем при счете, и дробей, которые образуются из натуральных чисел, нужны и другие, более «сложные» числа. Чтобы установить различия между «нормальными» и «сложными» числами, математики стали использовать символические названия: числа 1, 2, 3, 4, 5 и т. д. стали называться натуральными, а дроби, которые можно образовать из этих чисел, — рациональными.

Числа √2, 3√5, π , напротив, называются иррациональными, словно предупреждая об их нездоровой природе.

* * *

ИРРАЦИОНАЛЬНОСТЬ КОРНЯ ИЗ 2

В доказательстве подобных утверждений проявляется изумительная сила логических рассуждений математики. Так как существует бесконечное множество дробей и мы не можем проверить их все, то как мы можем быть уверены в том, что не существует дроби, которая при умножении на саму себя будет равна 2? Используем революционное изобретение древних греков — доказательство, то есть корректное логическое обоснование математического утверждения. Взяв за основу очевидный факт, посредством логических рассуждений, каждое из которых логически выводится из предыдущих, мы доказываем истинность другого, неочевидного, факта. Первое доказательство, о котором мы расскажем, приписывается самому Пифагору и звучит так. Заметим, что всякая дробь имеет эквивалентную ей несократимую дробь, числитель и знаменатель которой не имеют общих делителей. Если существует несократимая дробь (обозначим ее через p/ q), которая при умножении на саму себя равняется 2 (иными словами, p/ q· p/ q = 2), должно выполняться равенство р· р = 2· q· q. Покажем, что это невозможно. Если р· р = 2· q· q, то р· р— четное число; иными словами, оно в два раза больше некоторого другого числа. Так как квадрат нечетного числа — всегда нечетное число, рдолжно быть четным. Следовательно, число р в два раза больше некоторого другого числа, которое мы обозначим через k (иными словами, р = 2· k). Подставив это выражение в вышеуказанное равенство, получим 2· k·2· k = 2· q· q, или, что аналогично, 2· k· k = q· q. Следовательно, q· q— четное число, поэтому qтакже будет четным. Однако это невозможно, так как если дробь p/ qявляется несократимой, числитель и знаменатель не могут быть четными одновременно.