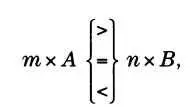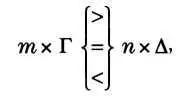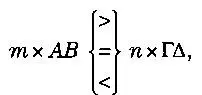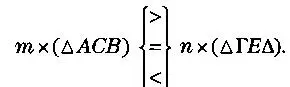Josep Carrera - Трехмерный мир. Евклид. Геометрия

А/B и Г/Δ.

Возникает вопрос: в каком случае мы можем сказать, что

А/B = Г/Δ, а когда А/B > Г/Δ ?

Теперь возьмем два произвольных множителя: множитель т для А и Г и n для В и А. При этом m х А и n х В — однородные величины, значит, их можно сравнивать; то же верно и для m х Г и n х Δ.

Следовательно, каково бы ни было значение множителей тип, каждый раз, когда мы имеем

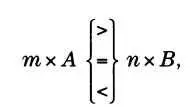
то имеем и

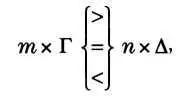
То есть А/B = Г/Δ

Если же у нас такая пара множителей при которых

m х A > n х B, но m х Г < n х Δ,то

А/B > Г/Δ

Из-за чего Евклиду понадобилось такое сложное определение? Из-за несоизмеримости. Рассмотрим одно и то же предложение в двух разных случаях: в первом отрезки будут соизмеримы, а во втором — нет.

Книга VI,предложение 1. Треугольники и параллелограммы, имеющие одинаковую высоту, относятся друг к другу как их основания.

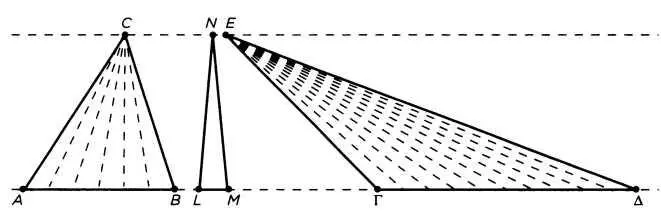
Рассмотрим доказательство этого предложения в случае соизмеримости. Если основания двух треугольников соизмеримы, то мы можем использовать общий измеритель для того, чтобы разложить их на равновеликие треугольники методом танграма (см. рисунок).

Если АВ и ΓΔ являются соизмеримыми основаниями двух треугольников, заключенных между одними и теми же параллельными, то существует общий отрезок LM, который делит основание АВ на т количество частей и основание ΓΔ — на п количество частей. Если мы соединим точки концов каждого из т отрезков, на которые LM делит основание АВ с вершиной С, и точки концов каждого из п отрезков, на которые LM делит основание ΓΔ с вершиной Е, то получим, соответственно, тип количество треугольников, равновеликих треугольнику LMN, где N — любая точка, взятая на прямой СЕ, параллельной А. Следовательно, АВС = m х (LMN), ΔΓΕ = m х (LMN). То есть

АВ/ΔΓ = (m х LM)/(n х LM) = (m х (ΔLMN))/(n х (ΔLMN)) = ΔABC/ΔAГ.

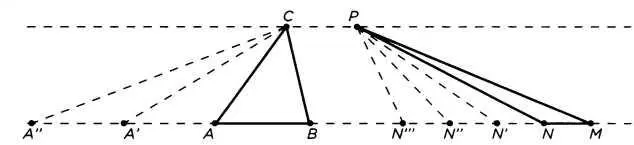
РИС. 3

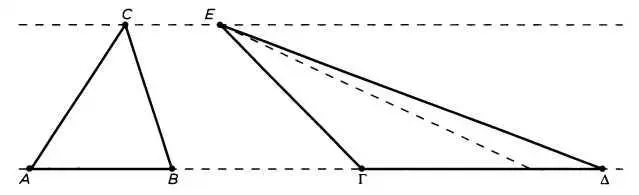
РИС. 4

Но если отрезки АВ и ΓΔ взяты произвольно, мы не можем знать, соизмеримы ли они. Действительно, любой отрезок имеет гораздо больше несоизмеримых ему отрезков, чем соизмеримых. Таким образом, доказательство, изложенное выше, является не общим, а, напротив, сугубо частным случаем. Рассмотрим теперь общее доказательство. Оно будет основано на следующей идее: если метод танграма нельзя применить внутри фигуры, это не значит, что его нельзя применить вне ее. Вместо того чтобы строить общий треугольник и помещать его в каждый из заданных, построим отрезки, равные каждому основанию, и соединим получившиеся точки с вершиной, как показано на рисунке 3. Таким образом, мы получим треугольники, кратные тип раз заданным:

ΔΑ"CΒ = m x (ΔΑCΒ), ΔΝ'" РМ = n x (ΔΝΡΜ).

Не нужно верить никаким предсказаниям, сделанным по гороскопам, основанным на дате рождения. Влияние звезд настолько трудно рассчитать, что на Земле нет никого, кто мог бы это сделать.

Евдокс

Теперь мы должны только убедиться, что из двух треугольников, заключенных между двумя параллельными прямыми (то есть одинаковой высоты), большая площадь — у того, у которого большее основание. Ответ, разумеется, утвердительный (см. рисунок 4). Основание АВ меньше основания ΓΔ. Следовательно, мы можем отложить АВ на ΓΔ (в «Началах» не объясняется понятие большего и меньшего, но интуитивно всегда используется верно: большее — то, что содержит часть, равную меньшему) и построить треугольник, равный АСВ, внутри ΓΕΔ.

Значит, площадь треугольника с большим основанием больше. Следовательно, если

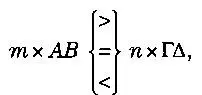
то

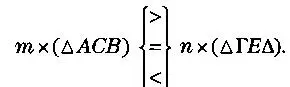
Теперь, применив определение Евдокса, мы получаем, что

АВ/ΓΔ = ΔАСВ/ΔΓΕΔ,

Ч.Т.Д.

В предыдущем примере мы установили равенство соотношений между парами величин различных видов: прямых в первом случае и площадей — во втором. Отсюда вытекает необходимость уточнения, которое содержится в определении 5 книги 5. Благодаря этим определениям Евклид располагал весьма полезным инструментом для получения конкретных геометрических результатов в области прямых и плоских многосторонних фигур. Эти результаты составляют основное содержание книги VI, в которой Евклид излагает в том числе предложения, указанные в следующей таблице. Это геометрическое ядро теории отношений.