Josep Carrera - Трехмерный мир. Евклид. Геометрия

Две стороны треугольника равны по длине третьей стороне (рисунок 3 на следующей странице).

Мы видим, что длина отрезков, составляющих ломаную линию, идущую от точки А до точки В, равна сумме длин сторон АС и СВ: АС + СВ = АС 1+ С 1А 1+ А 1С" 1+ С' 1В.

Если мы доведем эту последовательность до предела, ломаная линия сольется со стороной АВ, что доказывает ложность данного предложения. Гипотеза, верная до того, как ее «довели до предела», может оказаться ошибочной после этого.

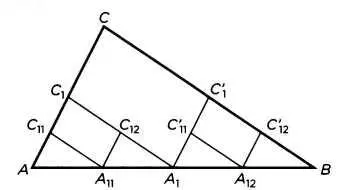
РИС. 3

Евклид открывает книгу XII двумя предложениями, которые устанавливают одну и ту же теорему для правильных многоугольников, вписанных в круг, и для круга.

Книга XII,предложение 1. Подобные многоугольники, вписанные в круги, будут относиться друг к другу как квадраты диаметров этих кругов.

Книга XII,предложение 2. Круги относятся друг к другу как квадраты их диаметров.

Первое предложение является прямым следствием теоремы Фалеса применительно к площадям, поскольку достаточно убедиться, что каждый из центральных треугольников, на которые раскладываются правильные многоугольники, подтверждает теорему Фалеса. Второе можно было бы доказать методом бесконечного ряда, но рассуждения, в которых используется понятие бесконечности, были неприемлемы для древнегреческих ученых (хотя в этом случае это было бы правильно). Евклид мог бы довести до предела предложение 2 книги XII таким образом: если для каждого многоугольника п вида п=2k справедливо соотношение

Р 1 n/d 2 1 =Р 2 n/d 2 2

и в самом крайнем случае Р 1 nравно S 1а Р 2 nравно S 2то есть от многоугольника переходим к кругу и получаем:

S 1/d 2 1= S 2/d 2 2

Ч.Т.Д.

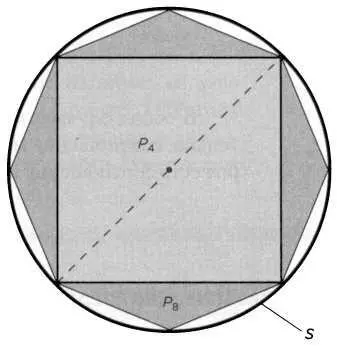
РИС. 4

Правильные многоугольники с 4,8,16,... сторонами все больше заполняют площадь круга.

Отказавшись от предела последовательности, нам остается только применить метод исчерпывания, то есть доказать, что квадрат, вписанный в круг, покрывает больше половины его площади. Если мы добавим треугольники, чтобы получить из квадрата восьмиугольник, получится больше половины площади, оставшейся после того, как мы уберем треугольник, и так далее. В какой-то момент вписанная в круг S многосторонняя фигура Р2k заполнит его так, что оставшееся пространство будет меньше любой другой предыдущей фигуры (см. рисунок 4).

Обратим внимание, что аналогично сказанному в предыдущей главе касательно сегмента параболы равнобедренный треугольник, который мы добавили к каждой стороне квадрата, чтобы получить восьмиугольник, покрывал более половины сегмента окружности, то есть четверть того, что остается от круга, когда мы убираем вписанный квадрат. Затем мы применили те же самые рассуждения к равнобедренным треугольникам, которые строятся на сторонах правильного восьмиугольника, чтобы получить 16-угольник, и так далее. Каждый раз фигуры покрывают более половины, что и необходимо для применения метода исчерпывания.

Пользуясь этим инструментом, Евклид выдвинул два предположения: соотношение площадей либо больше соотношения квадратов диаметров, либо меньше. Запишем оба случая:

(1) S 1/S 2< d 2 1/d 2 2или (2) S 1/S 2> d 2 1/d 2 2

В обоих случаях мы приходим к противоречию. Следовательно, соотношение между площадями и квадратами диаметров есть соотношение равенства.

В случае когда

S 1/S 2< d 2 1/d 2 2(1)

предположим, что существует такая площадь S < S 2, для которой

S 1/S 2= d 2 1/d 2 2

Затем рассмотрим площадь Е = S 2- S. Метод исчерпывания гарантирует, что существует некий многоугольник Р 2, вписанный в S 2, который заполняет его так, что S 2- Р 2< Е = S 2-S. Это приводит к неравенству S < Р 2. Теперь рассмотрим многоугольник Р 2, вписанный в круг (то есть Р 2< S 1, подобный P 2. Из предложения 1 книги XII мы знаем, что

P 1 n/P 2 n= d 2 1/d 2 2,

где n = 2 k. Исходя из общего понятия 1 мы имеем

P 1 n/P 2 n= d 2 1/d 2 2= S 1/S 2,

где S < Р 2и Р 2< S 1, что противоречит определению равенства соотношений (книга V, определение 5). Следовательно, первое допущение (1) неверно. Затем Евклид таким же образом рассматривает второе допущение

S 1/S 2> d 2 1/d 2 2(2)