Josep Carrera - Трехмерный мир. Евклид. Геометрия

«Предположения — это суждения, при наличии которых получается заключение благодаря тому, что они есть. И геометр не предполагает нечто ложное, как это утверждали некоторые, указывая, что не следует пользоваться ложными положениями, а геометр как раз и допускает ложное, когда про линию, не имеющую в длину фута, говорит, что она имеет эту длину, или про начерченную линию, не являющуюся прямой, говорит, что она прямая. Однако геометр ничего не выводит на основании того, что линия такая, какой он сам ее назвал, но выводит посредством того, что он этим имел в виду. Далее, всякий постулат и всякое предположение берется или как нечто целое, или как часть; определения же — ни как то, ни как другое».

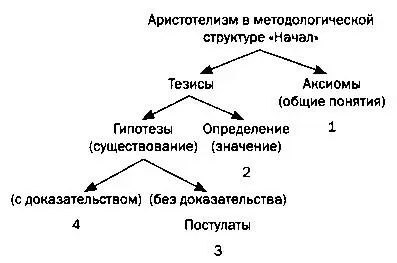
Аристотель установил метод построения научного рассуждения. Он кажется похожим на метод Платона, но это не так: Аристотель не делает различия между истинностью постулатов и истинностью, которая находится за пределами возможного познания. Есть истины, которые просто фиксируют факт существования и общие понятия с более широкой областью применения. Цепь рассуждений, подобно цепочке силлогизмов, идет от само собой разумеющейся истины к истине, доказываемой в теореме: у истины общих понятий и у истины теорем одна и та же природа. Однако Аристотелю требуются определения, в чем его мысль (ученика) опять расходится с представлениями Платона (учителя): необходимые и достаточные условия тесно связаны с терминами, применяемыми в определениях, и делают их правильными.

Философию науки — в частности, математики — Аристотеля можно представить в виде схемы.

Принято считать, что Евклид написал 13 книг с общим названием «Начала». Они изложены на койне с использованием символов, обозначающих геометрические понятия, в частности точки, величины и числа. Впоследствии к ним были добавлены еще две книги: книга XIV Гипсикла (ок. 190-120 до н.э.) и XV — неизвестного автора, возможно Исидора Милетского. Первое из более тысячи изданий «Начал» было сделано Эрхардом Ратдольтом (1442-1528) в Венеции в 1482 году, почти через 30 лет после публикации Библии Гуттенберга. Эрхард напечатал вариант с комментариями итальянского ученого Джованни Кампано (1220-1296), который, в свою очередь, опирался на перевод, сделанный английским монахом Аделярдом Батским (ок. 1080-1160). В первых четырех книгах не упоминается теория отношений. Они посвящены планиметрии, а не дидактике, и тем не менее сильно различаются.

— Книга I считается основной. В ней содержатся 23 определения, пять постулатов и пять общих понятий. Главная тема книги — теория треугольников. Представлены основы техники танграма для доказательств и построений с линейкой и циркулем. В конце книги — определение прямоугольных треугольников как таких, которые попадают под теорему Пифагора. Показаны дедуктивные возможности метода доведения до абсурда.

— Книга II содержит геометрическую алгебру, точнее элементарные алгебраические преобразования вида (х ± у)² = х² + у² ± 2ху, х² - у² = (х + у)(х — у) и их производные, но не с числами, а с размерами (отрезками), требующими построения; геометрическое решение линейных уравнений второго уровня из «Данных»; построение золотого сечения и теорема косинусов, обобщение теоремы Пифагора для непрямоугольных треугольников (остроугольных и тупоугольных). В книге есть два определения, а в заключении — предложение 14, недостающее звено для квадратуры многосторонних фигур.

— Книга III: геометрия окружности; И определений.

— Книга IV: построение правильных многоугольников при помощи линейки и циркуля: равностороннего треугольника (а также в первом предложении книги I), квадрата (предложения 6 и 7), пятиугольника (предложение И), шестиугольника (предложение 15) и 15-угольника (предложение 16). Содержит семь определений.

Авторство книг V и VI приписывается Евдоксу Книдскому. Эти тома легли в основу теоремы Фалеса для прямых и площадей многосторонних фигур и для вычисления площадей и объемов.

— Книга V имеет важнейшее значение для понимания древнегреческой геометрии в период Академии. Содержит 18 определений, среди которых особенно выделяются определения соотношения и пропорции. Устанавливает, для каких величин верна теория отношений.

— Книга VI содержит теоремы Фалеса, то есть теоремы о катетах прямоугольного треугольника, из которых выводится теорема Пифагора. Это очень важная книга. Одно из четырех ее определений, вероятно, не принадлежит Евклиду.