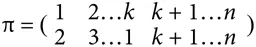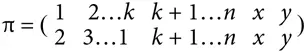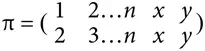Саймон Сингх - Симпсоны и их математические секреты

Хотя размерность 1,585 кажется нонсенсом, это имеет смысл в контексте процесса построения треугольника Серпинского, который начинается с обычного двумерного треугольника с большой видимой площадью, но последующее неоднократное (бесконечное число раз) удаление центрального треугольника означает, что полученный в результате треугольник Серпинского имеет нечто общее с сетью одномерных волокон или даже с совокупностью одномерных точек.

В эпизоде «Узник Бенды» Милейший Клайд Диксон пишет доказательство теоремы Килера (также известной как теорема Футурамы) на флуоресцентной зеленой доске. Вот расшифровка этого доказательства.

Во-первых, пусть π представляет собой k -циклическую перестановку на множестве [ n ] = {1, …, n }. Без потери общности запишем:

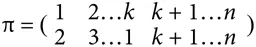
Пусть < a, b > означает перестановку, которая обеспечивает обмен содержимого a и b .

Согласно предположению, π образуется посредством k отдельных перестановок на множестве [ n ].

Введем два новых элемента и запишем:

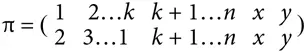
Для любого i = 1, …, k пусть σ представляет собой серию перестановок «слева-направо»:

σ = (< x , 1> < x , 2> … < x, i >) (< y, i + 1> < y, i + 2> … < y, k>) (< x, i + 1>) (< y , 1>)

Обратите внимание, что каждая перестановка приводит к обмену элемента из [ n ] на один из элементов { x, y }, а значит, все они отличны от перестановок в пределах множества [ n ], которые привели к образованию π, а также от < x, y >. Обычная проверка показывает, что теперь:

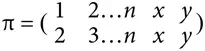
Другими словами, σ возвращает k -цикл в прежнее состояние и оставляет x и y на своих местах (без выполнения < x, y >).

Пусть теперь π представляет собой произвольную перестановку на множестве [ n ]: оно состоит из независимых (ненулевых) циклов, каждый из которых может быть поочередно возвращен в исходное состояние так, как показано выше, после чего x и y можно в случае необходимости поменять местами посредством < x, y >, что и требовалось доказать.

Я не смог бы написать эту книгу без поддержки сценаристов мультсериалов «Симпсоны» и «Футурама», которые нашли время для интервью и во многих случаях делали гораздо больше, чем от них требовалось, для того чтобы мне помочь. Я особенно признателен таким людям, как Дж. Стюарт Бернс, Эл Джин, Кен Килер, Тим Лонг, Майк Рейсс, Мэтт Селман, Патрик Веррон, Джош Вайнштейн и Джефф Уэстрбук. Дэвид Х. Коэн проявил невероятное дружелюбие и терпение и не жалел своего времени для меня с тех самых пор, как я написал ему первое электронное письмо еще в 2005 году. Должен также отметить, что Кен, Майк, Эл и Дэвид предоставили свои личные фотографии для включения в книгу, так же как и Майк Бэннен. Я искренне признателен компании Fox и Мэтту Грейнингу за разрешение использовать изображения из «Симпсонов» и «Футурамы».

Я благодарен Рони Брунн за информацию о математическом клубе, а также Эми Джо Перри, которая помогла организовать интервью и чувствовать себя как дома во время пребывания в Лос-Анджелесе. Я признателен также профессору Саре Гринволд и профессору Эндрю Нестлеру за то, что нашли время побеседовать со мной. Я советую читателям посетить их сайты, где они найдут еще много интересного о «Симпсонах» и «Футураме».

Это моя первая книга, написанная после того, как я стал отцом, поэтому я благодарю своего трехлетнего сына Хари Сингха, который провел прошедший год, стуча по клавиатуре моего компьютера и пуская слюни на рукопись книги, когда я этого не видел. Он был для меня лучшим отвлекающим фактором из всех возможных.

Когда я закрывался в своем кабинете, миссис Сингх (известная также как Анита Ананд) занималась важной работой: развлекая Хари, пекла кексы, рисовала картинки, ловила бабочек, запускала бумажного змея и играла в прятки. Когда Анита закрывалась в кабинете, чтобы писать свою книгу, Хари либо бегал без присмотра на улице, либо за ним присматривал кто-то другой. Я благодарен за это бабушке Сингх, дедушке Сингху, бабушке Ананд, Натали, Исааку и Махалии.