Иэн Стюарт - Математические головоломки профессора Стюарта

0,124999999999999999999999999999999999999999764,

что отличается от 1/8 менее чем на 10 −42.

В статье Шмуланда [22] Byron Schmuland, Random harmonic series, American Mathematical Monthly 110 (2003) 407–416. объясняется, почему эта вероятность так близка, но не равна в точности 1/8. Таким образом, очень правдоподобная гипотеза, выдвинутая на основе экспериментальных данных, оказывается ошибочной . Вот почему математики всегда настаивают на доказательствах, в точности так, как на них всегда настаивает Хемлок Сомс.

Во время обычной утренней прогулки в Равностороннем парке, что возле Мэрилбоун-роуд рядом с пабом «Пес и треугольник», я стал свидетелем любопытного инцидента и по прибытии на Бейкер-стрит, 222b не удержался от того, чтобы поделиться своими впечатлениями с коллегой.

– Сомс, я только что наблюдал любопытный…

– Инцидент. Вы видели в парке трех собак, – отозвался он, не моргнув глазом.

– Но как… конечно! На моих брюках грязь, и форма пятен и брызг указывает…

Сомс хмыкнул.

– Нет, Ватсап, мои дедуктивные выводы имеют другую основу. Они говорят мне не только, что вы видели трех собак в парке, но что эти собаки дрались.

– Так и есть! Но любопытный инцидент состоял не в этом. Наоборот, было бы любопытно, если бы собаки не стали драться.

– И правда. Нужно запомнить это замечание, Ватсап. Очень удачно сказано.

– Любопытно то, что предшествовало драке. Собаки появились одновременно в трех углах парка…

– Который представляет собой равносторонний треугольник со сторонами по 60 ярдов, – вставил Сомс.

– Ну да. И стоило собакам появиться, как каждая из них увидела противника – того, что находился от нее по часовой стрелке, – и без малейшего промедления рванула к нему.

– Все бежали с одинаковой скоростью 4 ярда в секунду.

– Склоняюсь перед вашей проницательностью. В результате все три собаки пробежали по одинаковым кривым дорожкам и одновременно столкнулись в центре парка. Никто и глазом моргнуть не успел, а они уже дрались, и мне пришлось их разнимать.

– Отсюда прорехи в вашем пальто и на брюках, а также следы зубов у вас на ноге. Я вижу, что они нанесены ирландским сеттером, ретривером и метисом бульдога с ирландским волкодавом. Хромым на переднюю левую лапу.

– Ах!

– В красном кожаном ошейнике. С колокольчиком. Который заржавел и больше не звонит. Хватило ли у вас наблюдательности, чтобы заметить, сколько времени ушло у собак на бег к точке встречи?

– Я забыл вынуть свои карманные часы, Сомс.

– Да ладно, Ватсап! Вы смотрите, но не видите . Однако в данном случае это время можно вычислить по уже установленным данным.

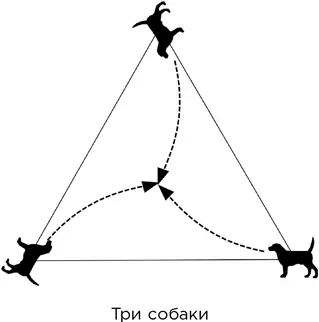
Считайте собак точечными объектами. Ответ см. в главе «Загадки разгаданные».

У лесничих есть один старый прием, позволяющий оценить высоту дерева, не влезая на него и не пользуясь геодезическими инструментами. Этот прием может послужить прекрасным средством взломать лед и оживить атмосферу на пикнике, если где-нибудь поблизости найдется подходящее дерево. Я познакомился с этим трюком в статье Тоби Бакленда [23] Toby Buckland, Digging deeper, Amateur Gardening (20 October 2012), p. 59. . Проделывать этот фокус рекомендуется в брюках.

Встаньте на некотором расстоянии от дерева спиной к нему. Наклонитесь и взгляните на дерево между своими ногами. Если вы не видите его вершины, отойдите подальше и повторяйте процедуру до тех пор, пока не увидите. Если вы легко видите ее, подойдите поближе на такое расстояние, чтобы вершина была едва видима. В этой точке расстояние от вас до основания дерева будет приблизительно равно его высоте.

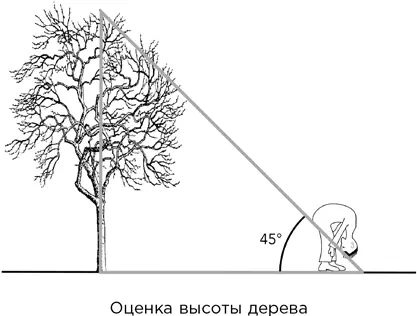
Эта методика, если ее можно так назвать, представляет собой простое приложение евклидовой геометрии. Она основана на том, что большинство людей может посмотреть между ногами назад и вверх под углом примерно 45°. Поэтому линия взгляда на вершину дерева оказывается гипотенузой равнобедренного прямоугольного треугольника, две другие стороны которого равны.

Очевидно, точность этого метода напрямую зависит от гибкости вашего тела, но для многих из нас он дает не слишком большую ошибку. Бакленд замечает: «Попробуйте, это дешевле, чем занятия йогой, и открывает нам взгляд на мир с такого ракурса, с какого большинство из нас не видело его с детства!»