Иэн Стюарт - Математические головоломки профессора Стюарта

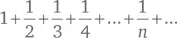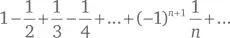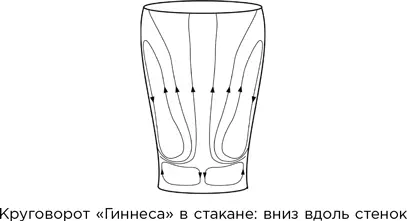
Ирландская команда нашла более точное объяснение, показав, что движение пива вызвано не прилипанием пузырьков к стенкам. Все дело в форме стакана. Темное пиво обычно пьют из стакана с изогнутыми стенками, который вверху шире, чем у донышка. Проделав гидродинамические расчеты и эксперименты, ученые выяснили, что, когда пузырьки вблизи стенки поднимаются, они идут прямо вверх, как и следовало ожидать. Но стенка уходит от вертикали, поэтому пузырьки, по существу, уходят от стенки прочь. Поэтому пиво у стенки плотнее, чем в середине стакана, и стремится опуститься вниз, увлекая за собой часть жидкости. Так что пиво в стакане циркулирует: вверх – в середине, вниз – вдоль стенок.

Пузырьки всегда поднимаются вверх относительно пива, но по краям пиво опускается быстрее, чем поднимаются пузырьки, и пузырьки опускаются вместе с ним. Пузырьки хорошо видны, в то время как движение пива заметить гораздо сложнее.

Дополнительную информацию см. в главе «Загадки разгаданные».

Бесконечный ряд

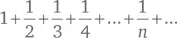
математики называют гармоническим рядом . Название отдаленно связано с музыкой, где обертоны колеблющейся струны имеют длины 1/2, 1/3, 1/4 и т. д. относительно основной для данной струны длины волны. Однако сама эта последовательность музыкального смысла не имеет. Известно, что это расходящаяся последовательность, то есть сумма первых n ее членов становится сколь угодно большой при достаточно большом n . Она расходится очень медленно, но все же расходится. Так, сумма первых 2 n членов последовательности больше, чем 1 + n /2. С другой стороны, если мы изменим знак каждого второго члена последовательности, получится знакопеременный гармонический ряд

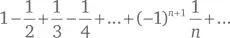
который является сходящимся. Его сумма равна ln 2, что составляет примерно 0,693.

Байрон Шмуланд заинтересовался тем, что происходит, если знак очередного члена последовательности выбирается случайным образом, бросанием монетки и присвоением знака плюс, к примеру, орлу, а знака минус – решке. Он доказал, что такая последовательность сходится с вероятностью 1 (гармонический ряд соответствовал бы выпадению ООООООО… до бесконечности, что происходит с нулевой вероятностью). Однако сумма такой последовательности зависит от последовательности бросков.

Возникает вопрос: какова вероятность получения какой-то определенной суммы? В принципе, суммой может быть любое действительное число, положительное или отрицательное, так что вероятность получения любого конкретного значения равна нулю (как обычно и бывает в случае «непрерывных случайных переменных»). В этом случае следует ввести распределение (или плотность) вероятности. Эта функция определяет вероятность попадания суммы в любой заданный диапазон величин, скажем, в промежуток между числами a и b . Эта вероятность равна площади под графиком функции распределения между x = a и x = b .

Для гармонического ряда, модифицированного при помощи монетки, распределение вероятности выглядит так, как показано на рисунке. Эта функция немного напоминает знакомую колоколовидную кривую, или нормальное распределение, но ее верхняя часть приплюснута. Это симметричная кривая, где замена левой стороны на правую соответствует замене орла на решку при бросании симметричной монетки.

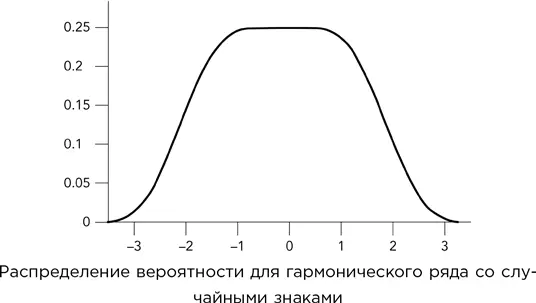
Эта задача – предметный урок «экспериментальной математики», в которой компьютерные расчеты используются для выдвижения интересных гипотез. Похоже, что центральный пик достигает высоты 0,25, то есть 1/4. Кроме того, значения функции при –2 и +2 равны 0,125, то есть 1/8. В 1995 г. Кент Моррисон предположил, что обе эти гипотезы верны, но в 1998 г. он изменил свое мнение и исследовал их подробнее. С точностью до десяти знаков после запятой плотность вероятности при x = 0 составляет 0,2499150393, то есть чуть меньше 1/4. Однако с той же точностью при x = 2 значение функции равно 0,1250000000, что по-прежнему очень похоже на 1/8. Но если провести расчет до 45 знаков после запятой, значение получится следующее: