Иэн Стюарт - Математические головоломки профессора Стюарта

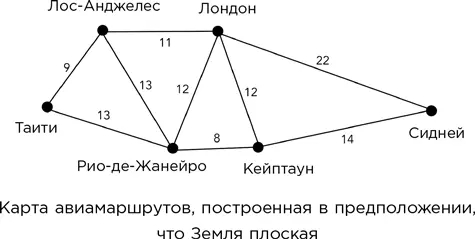
На рисунке показана триангуляция на базе шести крупных аэропортов. Сколько ни жонглируй числами, это единственная плоская фигура, сколько-нибудь разумно объединяющая все шесть аэропортов с учетом времени полета. Начнем, к примеру, с Лондона и добавим Кейптаун на расстоянии 12 часов. После этого поместим Рио-де-Жанейро и Сидней. Расположить их можно единственным образом, за исключением того, что всю карту можно зеркально отразить, поменяв местами право и лево, но не меняя никаких расстояний. Такая неоднозначность не имеет значения, а вот о том, чтобы Рио-де-Жанейро и Сидней находились по разные стороны от линии Лондон – Кейптаун, следует позаботиться. Если бы они находились по одну сторону от этой линии, то время полета между ними составляло бы примерно 11 часов, а на самом деле составляет 18. Далее можно добавить Лос-Анджелес и, наконец, Таити, опять же используя дополнительное время для устранения неоднозначности.

Теперь мы можем воспользоваться гипотезой плоской Земли и сделать предсказание. Расстояние от Таити до Сиднея, измеренное по этой карте, составляет примерно 35 часов. (Судя по ней, путь через Рио и Кейптаун проходит почти по прямой и сумма расстояний равна 35.) Таким образом, это минимальное время, которое, по идее, должен занимать перелет, не считая остановок.

Реальное же время перелета между этими пунктами – 8 часов. Даже допустив небольшие ошибки в расчетах, следует признать, что разница предсказанной и реальной продолжительности полета слишком велика и гипотеза плоской Земли должна быть отвергнута. Если включить в сеть намного больше аэропортов и взять более точные данные полетного времени, то можно выстроить базовую форму значительной части планеты очень точно – и по-прежнему в единицах часов полета. Чтобы установить масштаб, необходимо выяснить, с какой скоростью летают самолеты, или измерить по крайней мере одно расстояние каким-то другим способом.

Надо отметить, что каждый хорошо информированный адепт плоской Земли знаком с подобными аргументами и нестандартной физикой, которая их «объясняет». Может быть, какое-то искажающее поле изменяет геометрию пространства, так что буквальное измерение плоскости обычными мерами расстояния оказывается неверным. Это реально работает: азимутальная изогональная проекция Земли с Северного полюса дает именно такой эффект, и можно спокойно перенести все, включая и законы природы, с круглой Земли на плоскую, воспользовавшись проекцией на плоский диск. Конечно, если вам не нужна область вокруг Южного полюса. На логотипе ООН сделано именно так, и Общество плоской Земли постоянно использует его в качестве «доказательства» верности своих взглядов. Однако подобные выкладки тривиальны и бессмысленны, а изображение на логотипе логически эквивалентно круглой Земле с ее традиционной геометрией. Математически это всего лишь не слишком явный способ признать «она не плоская», в пределах ортодоксального смысла этой фразы. Так что измененная метрика и другие подобные отговорки на самом деле ничего не решают.

Действие ветра? Может быть, на самом деле от Таити к Сиднею постоянно дует сильный ветер? Такой ветер должен был бы достигать скорости 1200 км/ч, но дело обстоит еще хуже: прямой маршрут из Таити в Сидней очень близок маршрутам Таити – Рио – Кейптаун – Сидней, которые мы уже учли. Если можно попасть из Таити в Сидней по-настоящему быстро, воспользовавшись силой ветра, то путешествие, по крайней мере по одному из участков приведенного сложного маршрута, явно занимает слишком много времени.

Следующей линией обороны может быть стандартный прием всех отрицателей: это всеобщий заговор. Да, но чей? Времена, обозначенные на сайтах, где можно заказать авиабилеты, не могут быть слишком далеки от истины, поскольку миллионы людей ежедневно летают по воздуху, и большинство из них обратило бы внимание, если бы время полета по расписанию часто отличалось от реального в разы. Но все авиакомпании мира могли договориться летать по некоторым маршрутам медленнее, чем необходимо, так что бо́льшую часть моей схемы следовало бы ужать, сделав возможным перелет из Таити до Сиднея всего за 14 часов. Для этого пришлось бы поделить все времена по крайней мере на четыре, и получится, что обычный пассажирский самолет на самом деле мог бы добраться от Лондона до Сиднея всего за пять часов, если бы авиалиния не задерживала бы его специально для того, чтобы убедить нас в шарообразности Земли.