Иэн Стюарт - Математические головоломки профессора Стюарта

Более обширные данные вы можете найти на сайте http://ru.wikipedia.org/wiki/Список_египетских_пирамид

На ум приходят два наблюдения. Первое состоит в том, что приводить некоторые из этих углов с точностью до угловой секунды (а остальные до минуты) неразумно. Сторона основания Черной пирамиды Аменемхета III в Дашуре составляет 105 м, а высота – 75 м. Изменение угла наклона грани пирамиды на одну угловую секунду соответствует изменению высоты пирамиды на один миллиметр. Правда, следы ребер основания сохранились, как и некоторые фрагменты камней облицовки, но, учитывая общую степень сохранности пирамиды, вам трудно было бы оценить первоначальный наклон ее граней в пределах хотя бы 5° от истинной величины.

Второе, на что невольно обращаешь внимание, – это тот факт, что, хотя наклон граней пирамид немного варьируется (иногда даже в пределах одной пирамиды, как, к примеру, у Ломаной), у всех этих древних сооружений он близок к 54°. Почему?

В 1979 г. Р. Макмиллан [17] R.H. Macmillan, Pyramids and pavements: some thoughts from Cairo, Mathematical Gazette 63 (December 1979) 251–255. начал с того надежно установленного факта, что строители пирамид использовали для отделки своих сооружений с внешней стороны дорогостоящий облицовочный камень, к примеру белый турский известняк или гранит. Внутри они использовали более дешевые материалы: низкокачественный мокаттамский известняк, саманный кирпич и щебенку. Поэтому для них имело смысл всячески снижать количество каменной облицовки. Какой формы должна быть пирамида, если фараон желает, чтобы при заданной стоимости облицовочного камня монумент получился как можно больше? То есть какой угол наклона граней пирамиды к основанию позволяет получить максимальный объем при фиксированной суммарной площади четырех треугольных граней?

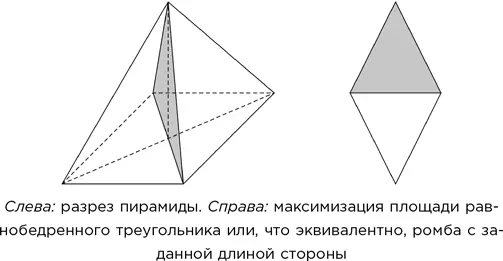
Вообще-то это прекрасное упражнение из области дифференциального исчисления, но эту задачу можно решить и проще, геометрически, если применить хитрый прием. Разрежем пирамиду пополам вертикальной плоскостью, проходящей через диагональ основания (серый треугольник). Получаем равнобедренный треугольник. Объем получившейся полупирамиды пропорционален площади этого треугольника, а площади наклонных граней полупирамиды пропорциональны длинам его соответствующих сторон. Поэтому задача эквивалентна поиску равнобедренного треугольника максимальной площади при фиксированной длине двух равных его сторон.

Зеркально отобразив треугольник относительно основания, получим, что наша задача эквивалентна поиску ромба максимальной площади при заданной длине стороны. Решением является квадрат (ориентированный диагональю по вертикали). Следовательно, углы при вершине каждой треугольной секции такого рода составляют 90°, а углы при основании – по 45°. Базовая тригонометрия подсказывает, что угол наклона грани пирамиды при этом равен

arctg √2 = 54°44′,

что близко к средней величине наклона грани у настоящих пирамид.

Макмиллан ничего не утверждает в отношении того, что говорят приведенные им расчеты о строительстве пирамид; его основная мысль заключается в том, что эта задача – показательный пример практического владения геометрией. Однако в Московском математическом папирусе приводится правило нахождения объема усеченной пирамиды (то есть пирамиды со срезанной верхушкой) и задача, из которой явствует, что египтяне понимали подобие. В нем объясняется также, как найти высоту пирамиды по ее основанию и наклону. Более того, и в этом папирусе, и в математическом папирусе Ринда объясняется, как найти площадь треугольника. Так что древнеегипетские математики вполне могли решить задачу Макмиллана.

Поскольку папируса, в котором содержался бы именно этот расчет, в нашем распоряжении нет, то нет и убедительных причин полагать, что эта задача действительно была решена в Древнем Египте. У нас нет никаких свидетельств того, что египтяне были заинтересованы в оптимизации формы своих пирамид. И даже если были, они вполне могли определить оптимальную форму экспериментально, при помощи глиняных моделей. Или просто произвести эмпирическую оценку. А может быть, форма постепенно эволюционировала в направлении наименьшей стоимости: строители и фараоны, они такие. В альтернативном варианте угол наклона грани мог определяться инженерными соображениями: считается, скажем, что необычная форма Ломаной пирамиды объясняется тем, что на середине строительства она начала разваливаться и строителям пришлось уменьшить крутизну граней. Тем не менее можно с уверенностью заявить, что этот небольшой математический пример имеет более непосредственное отношение к пирамидам, чем, скажем, скорость света.