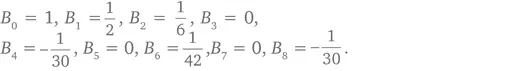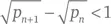В 1995 г. французский математик Оливье Рамаре доказал, что всякое четное число есть сумма не более шести простых чисел, а всякое нечетное число – сумма не более семи простых чисел. Среди специалистов стало крепнуть мнение, что проблема Гольдбаха для нечетных близка к решению, и они оказались правы: в 2013 г. Харальд Хельфготт объявил о доказательстве с применением связанных методов. Математики до сих пор проверяют его результат, но он, кажется, до сих пор держится. Из доказанной (будем надеяться) тернарной проблемы следует, что любое четное число есть сумма не более чем четырех простых чисел (если n – четное, то n – 3 – нечетное, а значит, сумма трех простых – q + r + s, поэтому n = 3 + q + r + s, то есть сумма четырех простых чисел). Это близко к бинарной проблеме Гольдбаха, но маловероятно, что ее удастся доказать полностью при помощи нынешних методов. Так что развиваться еще есть куда.
В математике есть свои тайны и загадки, и ученые, которые пытаются их разгадать, зачастую похожи на детективов. Они ищут зацепки, занимаются логической дедукцией, делают выводы и ищут доказательства собственной правоты. Как в делах Сомса, важнейший шаг в исследовании – это понять, как и с какого конца начать и какая линия рассуждений может привести к успеху. Во многих случаях мы до сих пор этого не знаем . Возможно, такое заявление звучит как признание собственного невежества, и в какой-то степени это действительно так. Но это заявление означает также, что новая математика до сих пор ждет своего открытия, а значит, эта область науки не вычерпана досуха. Простые числа – богатый источник правдоподобных предположений, о верности или ошибочности которых мы ничего не знаем. Вот некоторые из них. Во всех случаях pn обозначает n -е простое число.
Гипотеза Аго-Джуги
Число p является простым в том, и только том случае, если pB p − 1 + 1 делится на p , где B k – это k -е число Бернулли (Takashi Agoh, 1990 г.). Если вам по-настоящему интересно, информацию об этих числах можно посмотреть в Интернете. Приведем первые несколько вариантов:
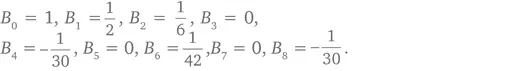
А вот другое, эквивалентное утверждение: число p является простым в том, и только том случае, если
[1 p − 1 + 2 p − 1 + 3 p − 1 + … + ( p − 1 ) p − 1 ] + 1
делится на p (Guiseppe Giuca, 1950).
Контрпример, если таковой существует, должен иметь по крайней мере 13 800 знаков (David Borwein, Jonathan Borwein, Peter Borwein and Roland Girgensohn, 1996).
Гипотеза Андрики
Если p n – это n -е простое число, то
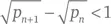
(Dorin Andrica, 1986).
Имран Гори использовал данные о наибольших промежутках между простыми числами, чтобы подтвердить эту гипотезу для n вплоть до 1,3002 × 10 16. На рисунке вы можете видеть зависимость √( p n +1) – √ p n от n для первых 200 простых чисел. Число 1 располагается в самом верху вертикальной оси, а все остальные пики, показанные на графике, – ниже. Они явно уменьшаются с увеличением n , но мы не можем быть уверены, что на каком-то очень большом n не наблюдается гигантский пик, превосходящий 1. Чтобы данная гипотеза оказалась ошибочной, где-то должен существовать особенно большой промежуток между двумя очень большими последовательными простыми числами. Это представляется весьма маловероятным, но и полностью исключить такой вариант пока невозможно.
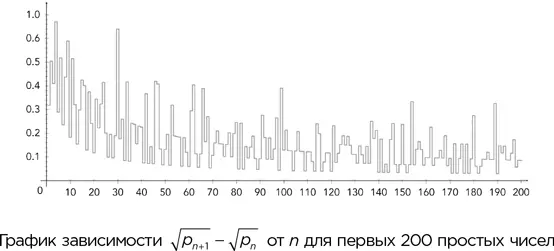
Гипотеза Артина о первообразных корнях
Любое целое число a , не равное −1 и не являющееся полным квадратом, есть первообразный корень по модулю бесконечного числа простых чисел. То есть всякое число от 1 до p − 1 есть некая степень a минус некое число, кратное p . Существуют конкретные формулы для количественного соотношения таких простых чисел по мере их увеличения (Emil Artin, 1927).
Гипотеза Брокара
При n > 1 существует по крайней мере четыре простых числа между p ² и p ² n +1(Henri Brocard, 1904). Ожидается, что это верно; более того, по идее должны быть верны куда более сильные утверждения.
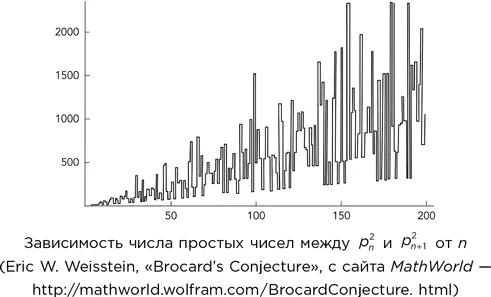
Гипотеза Крамера
Промежуток p n +1− p n между последовательными простыми числами для больших n не превосходит (ln p n )² с постоянным коэффициентом (Harald Cramér, 1936).
Читать дальше
Конец ознакомительного отрывка
Купить книгу