Иэн Стюарт - Математические головоломки профессора Стюарта

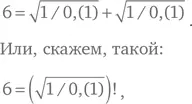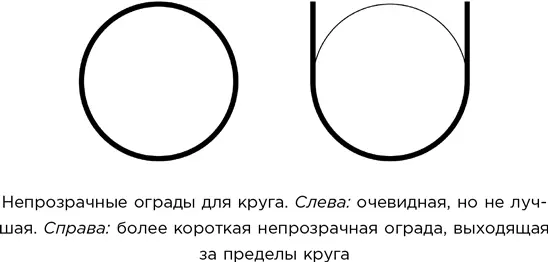
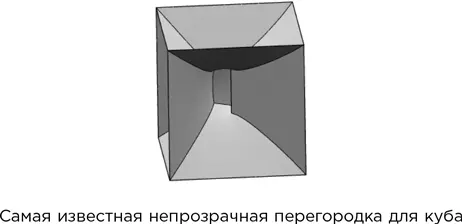
Кроме того, задача была расширена на трехмерное пространство: здесь ограда превращается в сложную поверхность. Самая известная непрозрачная ограда для куба образована из нескольких искривленных кусков.

No, pie are round. Chocolate are squared [14] Математическая шутка. По-английски формула πr 2 звучит очень похоже на фразу «Пирог квадратный». На что собеседник возражает: «Нет, пирог круглый. А вот шоколадка квадратная». – Прим. пер. .

– Сомс! Вот симпатичная головоломка. Она могла бы заинтересовать вас.

Хемлок Сомс положил кларнет, на котором только что исполнял боливийскую погребальную мелодию.

– Я в этом сомневаюсь, Ватсап.

Меланхоличное настроение преследовало моего друга уже несколько недель, и я намеревался во что бы то ни стало встряхнуть его.

– Задача в том, чтобы выразить целые числа 1, 2, 3 и т. д. с использованием не более чем…

– Четырех четверок, – сказал Сомс. – Я хорошо знаю эту задачу, Ватсап [15] W.W. Rouse Ball, Mathematical Recreations and Essays (11th edition), Macmillan, London 1939. .

Я решил, что не позволю отсутствию интереса с его стороны смутить меня.

– Основные арифметические символы позволяют таким образом добраться до 22. Знак квадратного корня повышает этот предел до 30. Знак факториала – до 112; знак возведения в степень – до 156…

– А субфакториала – до 877, – закончил за меня Сомс. – Это старая задачка, и ее уже давно выжали досуха.

– Что такое субфакториал, Сомс? – спросил я, но он уже уткнулся носом во вчерашний выпуск Daily Wail [16] Здесь обыгрывается название британской газеты Daily Mail. Daily Wail можно перевести как «Ежедневные вопли». – Прим. ред. .

Однако не прошло и минуты, как он вновь показался из-за газетного листа.

– Имейте в виду, Ватсап, существует множество возможных вариантов. Использование именно четверки дает нам значительную свободу, к тому же всего из одной четверки можно получить несколько весьма полезных чисел. К примеру, √4 = 2 и 4! = 24.

– А что означает здесь восклицательный знак? – поинтересовался я.

– Факториал. К примеру, 4! = 4 × 3 × 2 × 1. Что, как я уже сказал, равно 24.

– О-о.

– Эти дополнительные числа достаются нам бесплатно и существенно облегчают задачу. Но вот интересно… – его голос почти затих.

– Что интересно, Сомс?

– Интересно, как далеко можно продвинуться, если использовать четыре единицы .

Внутренне я ликовал, поскольку в нем явно пробудился интерес. А вслух сказал:

– Да, я понимаю. Теперь √1 = 1 и 1! = 1, так что «бесплатно» ничего не возникает. Это усложняет задачу, но делает ее, возможно, более достойной нашего внимания.

Он хмыкнул, и я поспешил реализовать свое крохотное преимущество. Лучший способ заинтересовать Сомса состоит в том, чтобы попробовать решить задачу самостоятельно и потерпеть неудачу.

– Понятно, что 1 = 1 × 1 × 1 × 1,

а также

2 = (1 + 1) × 1 × 1,

3 = (1 + 1 + 1) × 1,

4 = 1 + 1 + 1 + 1,

но выражение для 5 мне уже не дается.

Сомс поднял одну бровь.

– Вы могли бы рассмотреть выражение

5 = (1/0,1)/(1 + 1).

– Хм, хитро! – воскликнул я, но Сомс только фыркнул. – Но как насчет 6? – продолжал я. – Я вижу, как получить шестерку с использованием факториала:

6 = (1 + 1 + 1)! × 1.

На самом деле мне нужны только три единицы, но от всех лишних легко избавиться посредством умножения на них.

– Элементарно, – пробормотал он. – А рассматривали ли вы такой вариант, Ватсап?

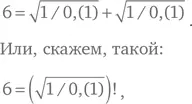
если вы настаиваете на использовании факториалов. Разумеется, чтобы использовать все четыре единицы, вы можете умножить на 1 × 1, или на 1/1, или прибавить 1–1.

Я непонимающе воззрился на формулу.

– Я узнаю десятичную точку, Сомс, но что означают скобки вокруг 1?

– Период, – ответил Сомс устало. – Нуль запятая 1 в периоде соответствует 0,11111… до бесконечности. Единица в периоде дает число, равное в точности 1/9. Разделив на это единицу, получим 9, корень из 9 равен 3…

– А дальше 3 + 3 = 6, – возбужденно вскричал я. – И еще, конечно,

7 = (1 + 1 + 1)! + 1

обходится без всяких корней. Но 8 – совсем другое дело…

– Обратите внимание, пожалуйста, – сказал Сомс.