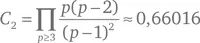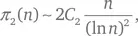Крамер доказал аналогичное утверждение, в котором вместо (ln p n )² фигурирует 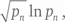 при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).
при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).
Гипотеза Фирузбахта
Величина 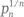 строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что
строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что 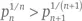 для любого n . Это утверждение верно для всех целых чисел вплоть до 4 × 1018.
для любого n . Это утверждение верно для всех целых чисел вплоть до 4 × 1018.
Первая гипотеза Харди – Литтлвуда
Пусть π2 ( x ) обозначает число простых чисел p ≤ x , таких, что p + 2 также простое число. Определим постоянную простых чисел-близнецов
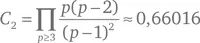
(где символ П указывает на произведение по всем простым числам p ≥ 3). Тогда гипотеза заключается в том, что
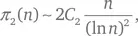
где знак ~ означает, что данное отношение стремится к 1 по мере того, как n становится сколь угодно большим (Godfrey Harold Hardy and John Edensor Littlewood, 1923).
Существует также вторая гипотеза Харди – Литтлвуда (см. ниже).
Гипотеза Гилбрейта
Начнем с простых чисел
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …
и вычислим разницу между соседними членами последовательности:
1, 2, 2, 4, 2, 4, 2, 4, 6, 2, …
Повторим те же вычисления для новой последовательности, не обращая внимания на знак, и продолжим в том же духе. Пять первых последовательностей будут выглядеть следующим образом:
1, 0, 2, 2, 2, 2, 2, 2, 4, …
1, 2, 0, 0, 0, 0, 0, 2, …
1, 2, 0, 0, 0, 0, 2, …
1, 2, 0, 0, 0, 2, …
1, 2, 0, 0, 2, …
Гилбрейт и Прот предположили, что первым членом каждой из этих последовательностей всегда будет 1, сколько бы раз мы ни повторяли процедуру (Norman Gilbreath, 1958, François Proth, 1978).
В 1993 г. Эндрю Одлизко проверил эту гипотезу для первых 3,4 × 1011 последовательностей.
Гипотеза Гольдбаха для четных чисел
Всякое четное целое число, большее 2, можно выразить как сумму двух простых чисел (Christian Goldbach, 1742).
Т. Оливейра-и-Силва проверил эту гипотезу на компьютере для n ≤ 1,609 × 10 18.
Гипотеза Гримма
Каждому элементу множества последовательных составных чисел можно поставить в соответствие отдельное простое число, которое является его делителем (C. A. Grimm, 1969).
К примеру, если взять составные числа 32, 33, 34, 35, 36, то им можно поставить в соответствие простые числа 2, 11, 17, 5, 3.
Четвертая проблема Ландау
В 1912 г. Эдмунд Ландау перечислил четыре фундаментальные проблемы, связанные с простыми числами и известные в настоящее время как проблемы Ландау. Первые три – это гипотеза Гольдбаха (см. выше), гипотеза о простых числах-близнецах (см. ниже) и гипотеза Лежандра (см. ниже). Четвертая проблема выглядит так: существует ли бесконечно много простых чисел p , таких что p − 1 является полным квадратом? То есть p = x ² + 1 для целого x .
Вот первые несколько таких чисел: 2, 5, 17, 37, 101, 197, 257, 401, 577, 677, 1297, 3137, 4357, 5477, 7057, 8101, 8837, 12 101, 13 457, 14 401 и 15 377. А вот пример побольше (но ни в коем случае не самый большой):
p = 1, 524, 157, 875, 323, 883, 675, 049, 535, 156, 256, 668, 194, 500, 533, 455, 762, 536, 198, 787, 501, 905, 199, 875, 019, 052, 101
x = 1, 234, 567, 890, 123, 456, 789, 012, 345, 678, 901, 234, 567, 890.
В 1997 г. Джон Фридлендер и Хенрик Иванец доказали, что существует бесконечно много простых чисел вида x 2+ y 4для целых x, y . Первые из этого ряда: 2, 5, 17, 37, 41, 97, 101, 137, 181, 197, 241, 257, 277, 281, 337, 401 и 457. Иванец доказал, что существует бесконечно много чисел вида x ² + 1, имеющих не более двух простых множителей.
Близко, но не то.
Гипотеза Лежандра
Адриан-Мари Лежандр предположил, что для любого положительного n существует простое число, лежащее между n ² и ( n + 1)². Это утверждение могло бы быть следствием из гипотезы Андрики (см. выше) и гипотезы Опперманна (см. ниже). Из гипотезы Крамера (см. выше) следует, что гипотеза Лежандра верна для всех достаточно больших чисел. Известно, что она верна вплоть до 1018.
Гипотеза Лемуана, или гипотеза Леви
Все нечетные целые числа, большие 5, могут быть представлены как сумма нечетного простого числа и удвоенного простого числа (Émile Lemoine, 1894, Hyman Levy, 1963).
Д. Корбитт подтвердил эту гипотезу вплоть до 10 9.
Гипотезы Мерсенна
В 1644 г. Марен Мерсенн объявил, что числа 2 n – 1 являются простыми для n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 и 257 и составными для всех остальных положительных целых n <257. Позже было показано, что Мерсенн допустил пять ошибок: n = 67 и 257 дают составные числа, а n = 61, 89, 107 дают простые. Гипотеза Мерсенна привела к созданию новой гипотезы Мерсенна и гипотезы Ленстры – Померанца – Вагстаффа, которые значатся в нашем перечне следующими.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

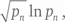 при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).
при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).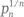 строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что
строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что 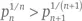 для любого n . Это утверждение верно для всех целых чисел вплоть до 4 × 1018.
для любого n . Это утверждение верно для всех целых чисел вплоть до 4 × 1018.